Zadanie nr 4075342
Jedynym rozwiązaniem wymiernym równania 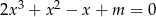 , gdzie
, gdzie 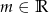 , jest liczba
, jest liczba 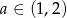 . Wyznacz liczbę
. Wyznacz liczbę 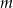 oraz pozostałe pierwiastki wielomianu.
oraz pozostałe pierwiastki wielomianu.
Rozwiązanie
Rozwiązania wymierne podanego równania są postaci 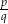 , gdzie
, gdzie 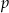 dzieli
dzieli 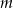 , a
, a 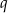 dzieli 2. Jedyna liczba tej postaci w przedziale
dzieli 2. Jedyna liczba tej postaci w przedziale 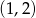 to
to 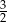 . Sprawdźmy kiedy jest to pierwiastek wielomianu.
. Sprawdźmy kiedy jest to pierwiastek wielomianu.
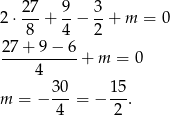
Równanie możemy więc zapisać w postaci.
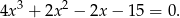
Dzielimy je teraz przez 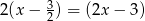 . My zrobimy to grupując wyrazy.
. My zrobimy to grupując wyrazy.
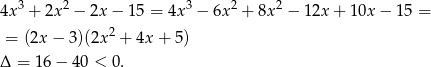
Zatem równanie nie ma innych pierwiastków.
Odpowiedź: