/Szkoła średnia/Równania/Wielomianowe/Stopnia 3/Z parametrem

Zadanie nr 4537864

Dodaj do ulubionych
Dodaj do rozwiązanych

Dla jakich wartości parametru 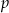p wielomian 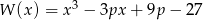3 W (x) = x − 3px + 9p − 27 ma trzy różne pierwiastki rzeczywiste?

Rozwiązanie

Po pierwsze sprawdźmy, czy przypadkiem nie uda nam się znaleźć jakiegoś pierwiastka niezależnego od 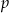p (te potęgi trójki jako współczynniki są aż nadto wymowne). Jak zwykle sprawdzamy dzielniki wyrazu wolnego, czyli liczby 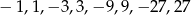− 1,1,− 3,3,− 9,9,− 27 ,27 . Pierwiastkiem okazuje się być 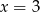x = 3 (jak już pisałem, ze względu na postać współczynników trudno było się tego nie spodziewać). Dzielimy teraz 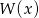W (x) przez (x − 3) . 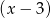My zrobimy to grupując wyrazy

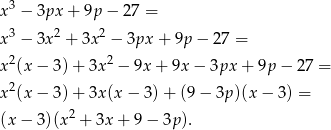
3 x − 3px + 9p − 27 = x 3 − 3x 2 + 3x 2 − 3px + 9p − 2 7 = x 2(x − 3)+ 3x 2 − 9x+ 9x − 3px + 9p− 27 = 2 x (x − 3)+ 3x (x − 3)+ (9− 3p)(x − 3) = (x − 3)(x 2 + 3x + 9− 3p).

Badamy teraz trójmian w nawiasie (ma mieć dwa różne pierwiastki)

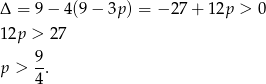
Δ = 9− 4(9− 3p) = − 27 + 12p > 0 12p > 27 9- p > 4.

To jeszcze nie koniec, bo żaden z pierwiastków tego trójmianu nie może być równy 3 (bo 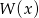W (x ) ma mieć 3 pierwiastki). Sprawdźmy kiedy tak jest (wstawiamy 3 do trójmianu)

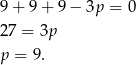
9+ 9+ 9− 3p = 0 27 = 3p p = 9.

Mamy zatem dodatkowy warunek 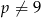p ⁄= 9 .  
Odpowiedź: 9 p ∈ (4,9)∪ (9 ,∞ )

Wersja PDF