Zadanie nr 4706101
Wyznacz wszystkie wartości parametru 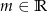 , dla których pierwiastki wielomianu
, dla których pierwiastki wielomianu 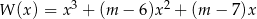 tworzą ciąg arytmetyczny.
tworzą ciąg arytmetyczny.
Rozwiązanie
Jeden pierwiastek danego równania widać gołym okiem – jest to 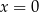 . Pozostałe pierwiastki są pierwiastkami równania kwadratowego
. Pozostałe pierwiastki są pierwiastkami równania kwadratowego
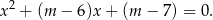
Sprawdźmy kiedy to równanie ma rozwiązania
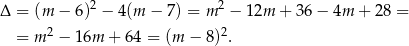
Równanie kwadratowe ma więc zawsze pierwiastki, przy czym dla 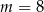 równanie ma postać
równanie ma postać
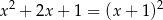
i ma tylko jedno rozwiązanie 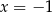 . Dwie liczby
. Dwie liczby 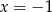 i
i 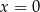 tworzą ciąg arytmetyczny (o różnicy
tworzą ciąg arytmetyczny (o różnicy 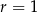 ), więc
), więc 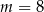 spełnia warunki zadania.
spełnia warunki zadania.
Jeżeli natomiast 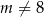 , to równanie kwadratowe ma dwa rozwiązania
, to równanie kwadratowe ma dwa rozwiązania 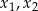 i na mocy wzorów Viète’a spełniają one warunki
i na mocy wzorów Viète’a spełniają one warunki
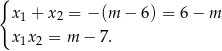
Nadal jednak nie wiemy, czy wyjściowe równanie ma dwa czy trzy pierwiastki – to zależy od tego, czy 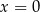 jest pierwiastkiem równania kwadratowego. Taka sytuacja ma miejsce tylko dla
jest pierwiastkiem równania kwadratowego. Taka sytuacja ma miejsce tylko dla 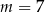 – wtedy równanie kwadratowe ma postać
– wtedy równanie kwadratowe ma postać
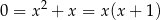
i jedyne niezerowe rozwiązanie to 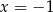 . Podobnie jak w przypadku
. Podobnie jak w przypadku 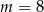 , w tej sytuacji też są spełnione warunki zadania.
, w tej sytuacji też są spełnione warunki zadania.
Pozostał najciekawszy przypadek, gdy wyjściowe równanie ma trzy różne pierwiastki: 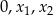 . Nadal nie wiemy w jakiej kolejności te liczby mają tworzyć ciąg arytmetyczny – tak naprawdę są dwie możliwości: albo
. Nadal nie wiemy w jakiej kolejności te liczby mają tworzyć ciąg arytmetyczny – tak naprawdę są dwie możliwości: albo 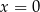 jest pomiędzy
jest pomiędzy 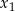 i
i 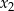 , albo
, albo 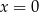 jest skrajnym wyrazem ciągu. W pierwszym przypadku mamy
jest skrajnym wyrazem ciągu. W pierwszym przypadku mamy
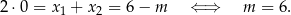
W drugim przypadku, możemy założyć, że arytmetyczny jest ciąg 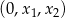 (jeżeli
(jeżeli 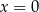 jest trzecim wyrazem ciągu, to możemy ustawić te trzy liczby w odwrotnej koejności i też otrzymamy ciąg arytmetyczny). Mamy wtedy
jest trzecim wyrazem ciągu, to możemy ustawić te trzy liczby w odwrotnej koejności i też otrzymamy ciąg arytmetyczny). Mamy wtedy
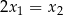
i wzory Viète’a przybierają postać
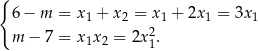
Z pierwszego równania mamy 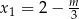 i wtedy drugie równanie przyjmuje postać
i wtedy drugie równanie przyjmuje postać
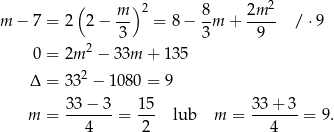
Odpowiedź: