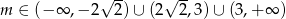/Szkoła średnia/Równania/Wielomianowe/Stopnia 3/Z parametrem

Zadanie nr 4818893

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz wszystkie wartości parametru 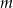m , dla którego wielomian 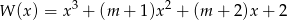W (x) = x3 + (m + 1)x2 + (m + 2)x + 2 ma trzy różne pierwiastki rzeczywiste.

Rozwiązanie

Specjalnie nie widać co zrobić z danych równaniem, więc spróbujmy nie przejmować się parametrem i sprawdźmy, czy jesteśmy w stanie znaleźć jakiś oczywisty pierwiastek wielomianu. Kandydaci na pierwiastki to dzielniki wyrazu wolnego, czyli liczby 1,-1,2,-2. Sprawdzając po kolei można zauważyć, że 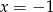x = −1 jest pierwiastkiem. Zatem wielomian można podzielić przez 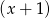(x + 1) . My dzielimy grupując wyrazy.

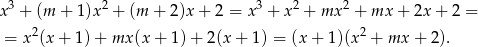
3 2 3 2 2 x + (m + 1)x + (m + 2)x+ 2 = x + x + mx + mx + 2x + 2 = = x 2(x+ 1)+ mx (x+ 1)+ 2(x+ 1) = (x + 1)(x 2 + mx + 2).

Sprawdźmy teraz, kiedy trójmian w nawiasie ma dwa pierwiastki

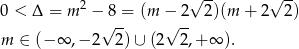
2 √ -- √ -- 0 < Δ = m − 8 = (m − 2 2)(m + 2 2) m ∈ (− ∞ ,− 2√ 2) ∪ (2√ 2,+ ∞ ).

To jeszcze nie koniec, bo trzeba sprawdzić, czy przypadkiem jeden z pierwiastków trójmianu nie jest równy 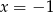x = − 1 (bo wtedy dane równanie 3-go stopnia nie będzie miało trzech pierwiastków). Sprawdźmy, kiedy 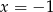x = − 1 jest pierwiastkiem trójmianu.

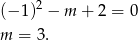
(−1 )2 − m + 2 = 0 m = 3.

 
Odpowiedź: √ -- √ -- m ∈ (− ∞ ,− 2 2)∪ (2 2,3)∪ (3,+ ∞ )

Wersja PDF