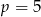/Szkoła średnia/Równania/Wielomianowe/Stopnia 3/Z parametrem

Zadanie nr 5446771

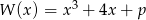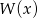Dany jest wielomian 3 W (x) = x + 4x + p , gdzie p jest liczbą pierwszą. Wyznacz p wiedząc, że W (x) ma pierwiastek całkowity.

Wersja PDF

Rozwiązanie

Pierwiastek całkowity danego wielomianu musi być dzielnikiem wyrazu wolnego, czyli 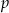p . Z drugiej strony 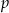p jest liczbą pierwszą, więc ma tylko 4 dzielniki: 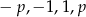− p,− 1,1 ,p . Sprawdzamy po kolei, czy któraś z tych liczb może być pierwiastkiem wielomianu

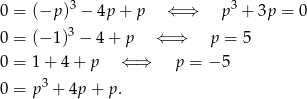
0 = (−p )3 − 4p + p ⇐ ⇒ p3 + 3p = 0 3 0 = (− 1) − 4 + p ⇐ ⇒ p = 5 0 = 1 + 4 + p ⇐ ⇒ p = − 5 3 0 = p + 4p + p.

Pierwsza, trzecia i czwarta równość są sprzeczne, bo 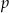p ma być liczbą pierwszą, więc w szczególności dodatnią. Pozostaje zatem druga równość, skąd p = 5 .  
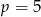Odpowiedź: p = 5

Wersja PDF