/Szkoła średnia/Równania/Wielomianowe/Stopnia 3/Z parametrem

Zadanie nr 7241047

Jednym z pierwiastków wielomianu 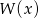W (x) stopnia trzeciego jest liczba 1, a suma pozostałych dwóch pierwiastków jest równa 0. Do wykresu tego wielomianu należy punkt 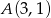A (3,1) . Wiedząc, że reszta z dzielenia wielomianu 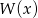W (x) przez dwumian 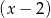(x − 2) jest równa 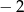− 2 , wyznacz wzór tego wielomianu.

Wersja PDF

Rozwiązanie

Z podanej informacji o pierwiastkach wiemy, że szukamy wielomianu postaci

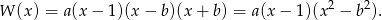
W (x) = a(x− 1)(x− b)(x + b) = a(x − 1 )(x 2 − b 2).

Wiemy ponadto, że 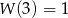W (3) = 1 , co daje równanie

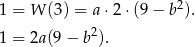
2 1 = W (3) = a ⋅2 ⋅(9− b ). 2 1 = 2a(9 − b ).

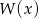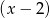Reszta z dzielenia wielomianu W (x ) przez (x − 2) jest równa 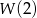W (2) (aby to zauważyć wystarczy podstawić 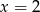x = 2 w równości 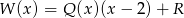W (x) = Q(x )(x− 2)+ R ). Wiemy więc dodatkowo, że 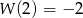W (2) = − 2 , co daje drugie równanie

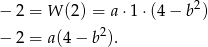
− 2 = W (2) = a ⋅1⋅ (4− b 2) 2 − 2 = a(4− b ).

Pozostało rozwiązać układ równań

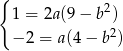
{ 2 1 = 2a(9− b ) − 2 = a (4− b 2)

Dzielimy pierwsze równanie przez drugie (żeby pozbyć się a ) i mamy

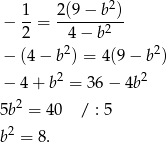
2 − 1-= 2(9-−-b-)- 2 4− b2 − (4 − b2) = 4 (9− b 2) − 4 + b2 = 3 6− 4b2 2 5b = 40 / : 5 b 2 = 8.

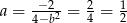Zatem a = -−-2 = 2 = 1 4−b 2 4 2 i wielomian 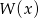W (x) jest równy

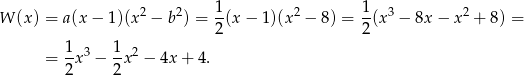
2 2 1- 2 1- 3 2 W (x ) = a(x − 1)(x − b ) = 2(x − 1)(x − 8) = 2(x − 8x − x + 8) = 1 1 = -x 3 − -x2 − 4x + 4. 2 2

 
Odpowiedź: W (x ) = 1x3 − 1x 2 − 4x + 4 2 2

Wersja PDF