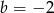Zadanie nr 7670961
Wiedząc, że wielomian 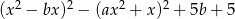 jest wielomianem stopnia 3 oraz 1 jest jego pierwiastkiem wyznacz
jest wielomianem stopnia 3 oraz 1 jest jego pierwiastkiem wyznacz  i
i 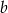 .
.
Rozwiązanie
Przekształćmy wzór wielomianu
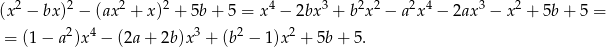
Skoro ma to być wielomian stopnia 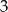 , to
, to 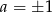 oraz
oraz 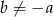 (żeby współczynnik przy
(żeby współczynnik przy 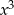 był niezerowy). Ponieważ 1 ma być pierwiastkiem tego wielomianu
był niezerowy). Ponieważ 1 ma być pierwiastkiem tego wielomianu
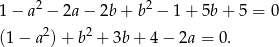
Uwzględniając fakt, że 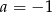 lub
lub 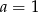 mamy dwa równania
mamy dwa równania
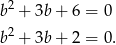
Pierwsze równanie nie ma rozwiązań, zatem 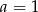 i pozostało rozwiązać drugie równanie.
i pozostało rozwiązać drugie równanie. 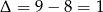 ,
, 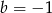 lub
lub 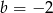 . Tylko drugie z tych rozwiązań spełnia warunek
. Tylko drugie z tych rozwiązań spełnia warunek 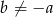 .
.
Odpowiedź: 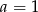 ,
,