/Szkoła średnia/Równania/Wielomianowe/Stopnia 3/Z parametrem

Zadanie nr 7908424

Znajdź wszystkie wartości parametru 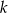k , dla których równanie 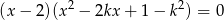(x − 2)(x 2 − 2kx + 1− k2) = 0 ma więcej niż jeden pierwiastek.

Wersja PDF

Rozwiązanie

Jeden pierwiastek mamy podany na tacy: 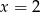x = 2 . Po podzieleniu przez 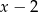x − 2 mamy równanie kwadratowe.

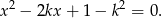
x2 − 2kx + 1 − k2 = 0.

Sprawdźmy kiedy ma ono pierwiastki

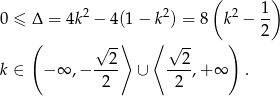
( ) 0 ≤ Δ = 4k2 − 4(1− k2) = 8 k2 − 1- 2 ( √ -⟩ ⟨ √ -- ) k ∈ − ∞ ,− ---2 ∪ --2-,+ ∞ . 2 2

Nie jest to jeszcze koniec, bo musimy sprawdzić, czy przypadkiem jedynym pierwiastkiem tego równania kwadratowego nie jest 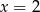x = 2 . Tak jednak nie jest, bo równanie ma jeden pierwiastek dokładnie dla 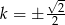√- k = ± -22- i jest on równy

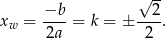
√ -- −b 2 xw = 2a-= k = ± -2--.

 
Odpowiedź: ( √-⟩ ⟨ √- ) -2- -2- k ∈ −∞ ,− 2 ∪ 2 ,+ ∞

Wersja PDF