Zadanie nr 8144601
Wyznacz wartość parametru 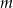 , dla którego równanie
, dla którego równanie
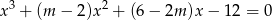
ma trzy pierwiastki 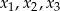 spełniające warunki
spełniające warunki 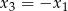 oraz
oraz 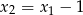 .
.
Rozwiązanie
Sposób I
Z podanych informacji wiemy, że dany wielomian musi mieć postać
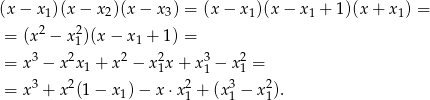
Porównując teraz współczynniki ze współczynnikami danego wielomianu otrzymujemy układ równań
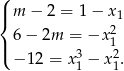
(Układ ten mogliśmy też otrzymać stosując wzory Viète’a dla równania stopnia 3).
Możemy ten układ rozwiązać na różne sposoby, my podstawimy 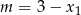 z pierwszego równania do drugiego
z pierwszego równania do drugiego
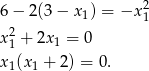
Rozwiązanie 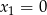 jest sprzeczne z trzecim równaniem układu, zatem
jest sprzeczne z trzecim równaniem układu, zatem 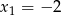 i mamy
i mamy 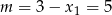 . Łatwo sprawdzić (choć nie musimy tego robić), że dla tych wartości wszystko jest OK, tzn. liczby
. Łatwo sprawdzić (choć nie musimy tego robić), że dla tych wartości wszystko jest OK, tzn. liczby 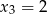 i
i 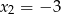 spełniają zależności z treści zadania.
spełniają zależności z treści zadania.
Sposób II
Na początku nie widać specjalnie jak się zabrać za to zadanie, więc spróbujmy zignorować to, że w równaniu jest parametr i poszukajmy pierwiastków wśród dzielników wyrazu wolnego. Sprawdzając po kolei 1,-1,2,-2 można zauważyć, że 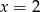 jest pierwiastkiem:
jest pierwiastkiem:
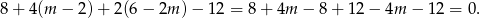
Zatem wielomian jest podzielny przez dwumian 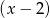 – wykonujemy to dzielenie. My zrobimy to grupując wyrazy.
– wykonujemy to dzielenie. My zrobimy to grupując wyrazy.
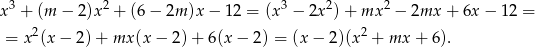
Zastanówmy się teraz co dalej. Wiemy, że jeden z pierwiastków to 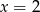 , ale nie wiemy który. Musimy więc rozważyć 3 przypadki.
, ale nie wiemy który. Musimy więc rozważyć 3 przypadki.
Jeżeli 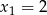 to z podanych równości mamy
to z podanych równości mamy 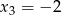 i
i 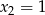 . To jednak nie jest możliwe, bo na mocy wzorów Viète’a iloczyn pierwiastków trójmianu w nawiasie jest równy 6.
. To jednak nie jest możliwe, bo na mocy wzorów Viète’a iloczyn pierwiastków trójmianu w nawiasie jest równy 6.
Jeżeli 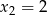 to z podanych równości mamy
to z podanych równości mamy 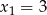 i
i 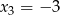 . Jak poprzednio, to nie jest możliwe, bo na mocy wzorów Viète’a iloczyn pierwiastków trójmianu w nawiasie jest równy 6.
. Jak poprzednio, to nie jest możliwe, bo na mocy wzorów Viète’a iloczyn pierwiastków trójmianu w nawiasie jest równy 6.
Jeżeli natomiast 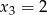 to
to 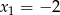 oraz
oraz 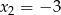 i jest OK, bo iloczyn tych liczb to 6. Korzystając ponownie ze wzorów Viète’a mamy
i jest OK, bo iloczyn tych liczb to 6. Korzystając ponownie ze wzorów Viète’a mamy
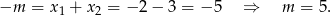
Możemy sprawdzić, że pierwiastkami równania 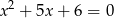 rzeczywiście są liczby
rzeczywiście są liczby 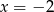 i
i 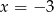 .
.
Odpowiedź: