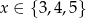/Szkoła średnia/Równania/Wielomianowe/Stopnia 3/Z parametrem

Zadanie nr 8700545

Dany jest wielomian 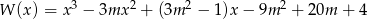3 2 2 2 W (x) = x − 3mx + (3m − 1)x − 9m + 20m + 4 . Wykres tego wielomianu, po przesunięciu o wektor → u = [− 3,0] , przechodzi przez początek układu współrzędnych. Wyznacz wszystkie pierwiastki wielomianu W .

Wersja PDF

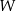Rozwiązanie

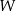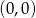Jeżeli wykres wielomianu W po przesunięciu o wektor → u = [− 3,0] przechodzi przez punkt (0,0) , to wykres wielomianu przed przesunięciu musiał przechodzić przez punkt 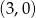(3,0) (bo przesuwamy o 3 jednostki w lewo). Mamy zatem W (3 ) = 0 .

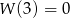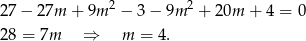
27 − 27m + 9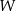m 2 − 3− 9m 2 + 2 0m + 4 = 0 28 = 7m ⇒ m = 4.

Wielomian W ma więc wzór

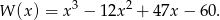
3 2 W (x) = x − 12x + 47x − 60.

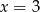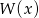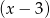Znamy ponadto jeden z pierwiastków tego wielomianu: x = 3 . Dzielimy więc W (x) przez (x − 3) – my zrobimy to grupując wyrazy.

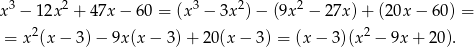
x3 − 12x2 + 47x − 60 = (x3 − 3x2)− (9x2 − 27x) + (20x − 60) = 2 2 = x (x − 3) − 9x(x − 3) + 20 (x− 3) = (x − 3)(x − 9x + 20 ).

Rozkładamy jeszcze trójmian w drugim nawiasie.

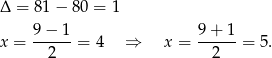
Δ = 81 − 80 = 1 x = 9-−-1-= 4 ⇒ x = 9-+-1-= 5. 2 2

Wielomian 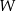W ma więc 3 pierwiastki: {3,4,5} .  
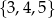Odpowiedź: x ∈ { 3,4,5}

Wersja PDF