/Szkoła średnia/Równania/Wielomianowe/Stopnia 3/Z parametrem

Zadanie nr 9164524

Pierwiastkami wielomianu 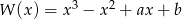3 2 W (x ) = x − x + ax + b są tylko dwie liczby: 2 oraz (-3).

  • Oblicz a i b .
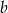  • Zapisz wielomian w postaci czynników liniowych.
Wersja PDF

Rozwiązanie

  • Ponieważ 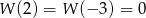W (2) = W (− 3) = 0 , mamy układ równań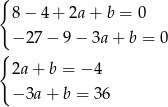
    { 8− 4+ 2a+ b = 0 { − 27− 9− 3a+ b = 0 2a+ b = − 4 − 3a+ b = 36

    Odejmując od pierwszego równania drugie (żeby skrócić 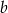b ), otrzymujemy 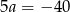5a = − 4 0 , czyli 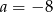a = −8 . Stąd b = 12 .  
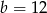    Odpowiedź: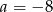 a = − 8 , b = 12

  •  

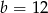
    Sposób I

    Wiemy, że 2 i (-3) są pierwiastkami, dzielimy więc wielomian

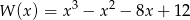
    W (x) = x3 − x2 − 8x + 1 2

    przez 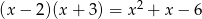(x− 2)(x+ 3) = x2 + x − 6 . My zrobimy to grupując czynniki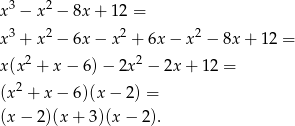

    x 3 − x 2 − 8x + 12 = 3 2 2 2 x + x − 6x − x + 6x− x − 8x + 12 = x (x2 + x− 6)− 2x2 − 2x + 12 = 2 (x + x − 6 )(x − 2) = (x − 2 )(x + 3)(x− 2).

    Sposób II

    Skoro wiemy, że dany wielomian nie ma innych pierwiastków niż 2 i (-3), wystarczy sprawdzić, który z nich jest podwójny. Robi się to bardzo prosto przy pomocy pochodnej – pierwiastki wielokrotne są też pierwiastkami pochodnej. Fakt ten to proste zadanie na wzór na pochodną iloczynu. Liczymy

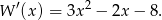
    ′ 2 W (x ) = 3x − 2x − 8.

    Łatwo sprawdzić, że 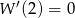W ′(2) = 0 , co oznacza, że 2 jest pierwiastkiem podwójnym wielomianu W (x) .  
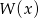    Odpowiedź: W (x) = (x − 2 )2(x + 3)

Wersja PDF