Zadanie nr 7355961
Jeżeli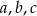 
i 
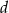są długościami kolejnych boków czworokąta, to przekątne tego czworokąta są prostopadłe wtedy i tylko wtedy, gdy 
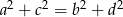. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Czworokąt, którego dwa przeciwległe boki mają długości 7 i 24, a dwa pozostałe boki mają długości 15 i 20 ma prostopadłe przekątne. | P | F |
Czworokąt, w którym długości kolejnych boków są równe: 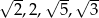 ma prostopadłe przekątne. | P | F |
Rozwiązanie
Naszkicujmy czworokąt, żeby nie pogubić się w oznaczeniach jego boków.
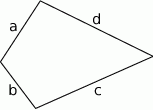
Sprawdzamy najpierw czworokąt, w którym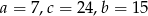 
i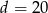 
.
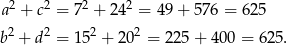
To oznacza, że przekątne tego czworokąta rzeczywiście są prostopadłe.
Teraz sprawdzamy czworokąt, w którym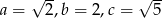 
i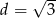 
.
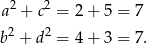
To oznacza, że przekątne tego czworokąta też są prostopadłe.
Odpowiedź: P, P
