/Szkoła podstawowa/Zadania testowe/Bloki zadań/Dana procedura

Zadanie nr 2989624

Dodaj do ulubionych
Dodaj do rozwiązanych

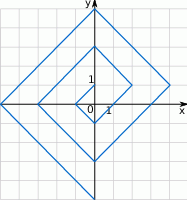
Zaczynając od punktu 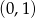(0,1) budujemy łamaną, której część składającą się z 10 odcinków przedstawiono na rysunku. Kolejne odcinki łamanej numerujemy kolejnymi liczbami naturalnymi. Pierwszy odcinek łamanej ma długość √ 2- .

PIC

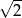Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Łamana złożona z 8 początkowych odcinków ma długość 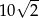√ -- 1 0 2 .PF
Długość setnego odcinka jest równa 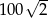√ -- 1 00 2 . PF

Rozwiązanie

Zauważmy, że suma długości 8 początkowych odcinków jest równa długości

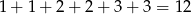
1+ 1+ 2+ 2+ 3+ 3 = 12

przekątnych kwadratu o boku 1. Jest więc równa 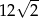√ -- 12 2 .

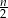Z rysunku widać, że jeżeli odcinek ma numer parzysty n , to jego długość jest równa n 2 długościom przekątnych kwadratu o boku długości 1. Jest więc równa

n- √ -- 2 ⋅ 2.

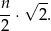
W takim razie setny odcinek ma długość 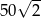√ -- 50 2 .  
Odpowiedź: F, F

Wersja PDF