Zadanie nr 5895382
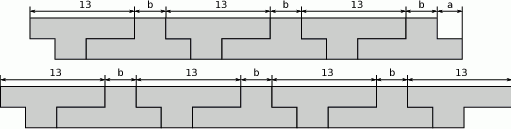
Na rysunkach przedstawiono kształt i sposób układania płytek oraz niektóre wymiary w centymetrach.
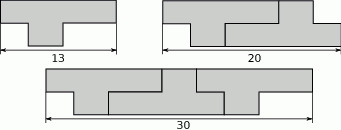
Niech  będzie całkowitą szerokością wzoru ułożonego z
będzie całkowitą szerokością wzoru ułożonego z  płytek. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
płytek. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Jeżeli 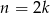 jest liczbą parzystą, to jest liczbą parzystą, to 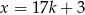 . . | P | F |
Jeżeli 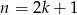 jest liczbą nieparzystą, to jest liczbą nieparzystą, to 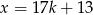 | P | F |
Rozwiązanie
Oznaczmy przez 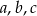 szerokości odpowiednio lewego ramienia płytki, środkowej części płytki oraz prawego ramienia płytki.
szerokości odpowiednio lewego ramienia płytki, środkowej części płytki oraz prawego ramienia płytki.
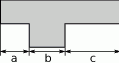
Wzór złożony z dwóch płytek jest szerszy od jednej płytki o 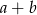 , więc
, więc
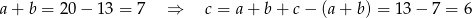
Wzór złożony z trzech płytek jest szerszy od dwóch pojedynczych płytek o 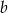 , więc
, więc
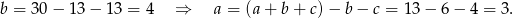
Zauważmy, że jeżeli 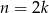 jest liczbą parzystą, to wzór składający się z
jest liczbą parzystą, to wzór składający się z 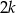 płytek ma szerokość równą sumie szerokości
płytek ma szerokość równą sumie szerokości 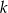 całych płytek,
całych płytek, 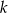 części środkowych oraz jednego odcinka długości
części środkowych oraz jednego odcinka długości  .
.
Zatem w tym przypadku
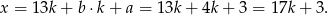
Jeżeli 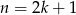 jest liczbą nieparzystą, to wzór składający się z
jest liczbą nieparzystą, to wzór składający się z 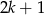 płytek ma szerokość równą szerokości
płytek ma szerokość równą szerokości 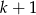 całych płytek, oraz
całych płytek, oraz 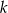 części szerokości
części szerokości 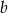 , czyli
, czyli
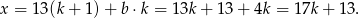
Odpowiedź: P, P

