Zadanie nr 9549614
Wykaż, że dla dowolnych punktów płaszczyzny 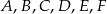 spełniona jest równość.
spełniona jest równość.
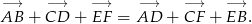
Rozwiązanie
Najpierw szkicowy rysunek.
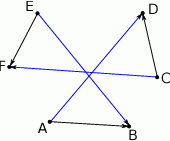
Sposób I
Wprowadźmy na płaszczyźnie układ współrzędnych oraz niech
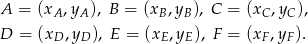
Wtedy
![−→ − → −→ L = AB + CD + EF = = [xB − xA ,yB − yA ]+ [xD − xC ,yD − yC ]+ [xF − xE ,yF − yE] = = [xB + xD + xF − xA − xC − xE,yB + yD + yF − yA − yC − yE] − → −→ − → P = AD + CF + EB = = [xD − xA ,yD − yA]+ [xF − xC,yF − yC ]+ [xB − xE ,yB − yE] = = [xD + xF + xB − xA − xC − xE,yD + yF + yB − yA − yC − yE].](https://img.zadania.info/zad/9549614/HzadR2x.gif)
Zatem rzeczywiście 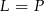 .
.
Sposób II
Używając notacji 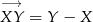 (możemy myśleć, że po lewej i prawej stronie są współrzędne), mamy
(możemy myśleć, że po lewej i prawej stronie są współrzędne), mamy
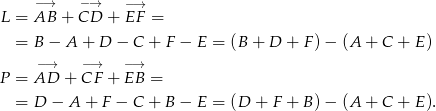
Zatem rzeczywiście 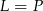 . Zauważmy, że przy tym sposobie rozwiązania nie miało znaczenia, że dane punkty leżą na płaszczyźnie.
. Zauważmy, że przy tym sposobie rozwiązania nie miało znaczenia, że dane punkty leżą na płaszczyźnie.
Sposób III
Tym razem użyjemy odrobinę więcej geometrii. Patrzymy na obrazek i zauważamy, że