/Szkoła podstawowa/Zadania testowe/Funkcje/Różne

Zadanie nr 5573290

Dodaj do ulubionych
Dodaj do rozwiązanych

O funkcji liniowej 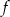f wiadomo, że 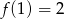f (1) = 2 . Do wykresu tej funkcji należy punkt 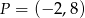P = (−2 ,8) . Wzór funkcji 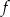f to
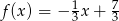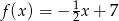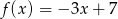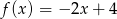
A) f(x ) = − 13x + 73 B) f(x) = − 12x + 7 C) f(x ) = − 3x + 7 D) f (x) = − 2x + 4

Rozwiązanie

Sposób I

Sprawdzamy, w którym wzorze otrzymamy 2 po podstawieniu 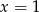x = 1 . Tak jest tylko w przypadku wzorów

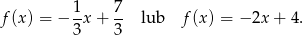
1 7 f (x) = − --x+ -- lub f(x ) = − 2x + 4. 3 3

Sprawdzamy teraz, że tylko w przypadku drugiego wzoru otrzymamy 8 po podstawieniu 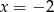x = − 2 .

Sposób II

Szukamy funkcji postaci 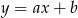y = ax+ b . Podstawiając współrzędne podanych punktów, mamy

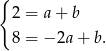
{ 2 = a+ b 8 = − 2a+ b.

Odejmując te równości stronami otrzymujemy

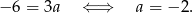
− 6 = 3a ⇐ ⇒ a = − 2.

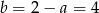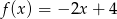Stąd b = 2 − a = 4 . Zatem f(x) = − 2x+ 4 .  
Odpowiedź: D

Wersja PDF