Zadanie nr 8544533
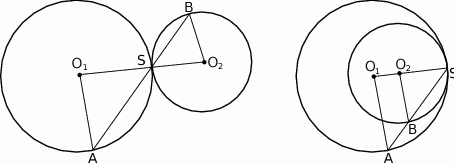
Przez punkt styczności dwóch okręgów poprowadzono sieczną. Udowodnij, że wypukłe kąty środkowe oparte na łukach wyznaczonych przez tę sieczną na okręgach mają równe miary.
Rozwiązanie
Jeżeli połączymy środki 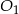 i
i 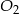 danych okręgów, to prosta ta przejdzie przez punkt
danych okręgów, to prosta ta przejdzie przez punkt 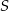 styczności tych okręgów.
styczności tych okręgów.
Zatem
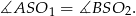
Ponieważ trójkąty 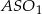 i
i 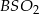 są równoramienne, oznacza to, że
są równoramienne, oznacza to, że