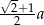Zadanie nr 1723380
Z wierzchołków kwadratu o boku  , jako ze środków zakreślono 4 okręgi o promieniu
, jako ze środków zakreślono 4 okręgi o promieniu 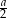 . Znajdź promienie okręgów stycznych do tych czterech okręgów jednocześnie.
. Znajdź promienie okręgów stycznych do tych czterech okręgów jednocześnie.
Rozwiązanie
Typowe zadanie, w którym wystarczy wykonać duży rysunek, a dalej rozwiązuje się już samo.
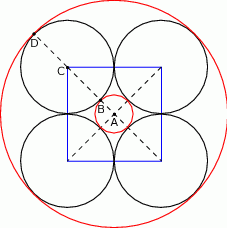
Widać, że są dwa okręgi styczne do czterech opisanych okręgów: jeden w środku i jeden na zewnątrz. Promień mniejszego z nich to po prostu różnica połowy długości przekątnej kwadratu i promienia okręgu o środku w wierzchołku kwadratu, czyli
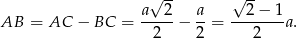
Podobnie wyliczamy długość promienia większego okręgu
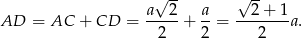
Odpowiedź: 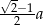 oraz
oraz