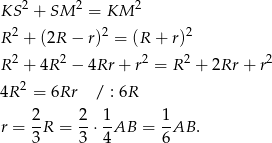Zadanie nr 4538957
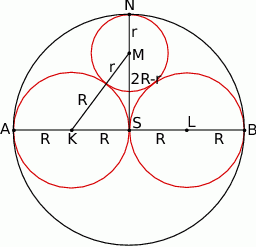
Dany jest okrąg o średnicy  i środku
i środku  oraz dwa okręgi o średnicach
oraz dwa okręgi o średnicach 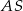 i
i 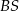 . Okrąg o środku
. Okrąg o środku 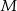 i promieniu
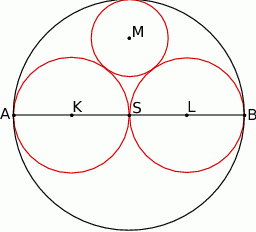
i promieniu  ma z każdym z danych okręgów dokładnie jeden punkt wspólny (zobacz rysunek). Wykaż, że
ma z każdym z danych okręgów dokładnie jeden punkt wspólny (zobacz rysunek). Wykaż, że 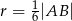 .
.
Rozwiązanie
Niech 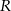 będzie promieniem okręgów o środkach
będzie promieniem okręgów o środkach 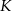 i
i 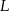 , a
, a  niech będzie promieniem okręgu o środku
niech będzie promieniem okręgu o środku 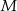 .
.
Zauważmy, że przy tych oznaczeniach 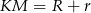 i
i
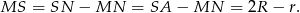
Piszemy teraz twierdzenie Pitagorasa w trójkącie 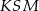 .
.