/Szkoła średnia/Geometria/Geometria analityczna/Równanie prostej

Zadanie nr 1906633

Dodaj do ulubionych
Dodaj do rozwiązanych

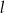Prosta l , na której leży punkt 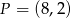P = (8,2) , tworzy z dodatnimi półosiami układu współrzędnych trójkąt prostokątny o polu równym 36. Wyznacz równanie prostej l .

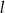Rozwiązanie

Szkicujemy opisaną sytuację.

PIC

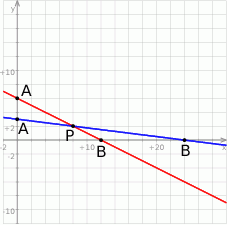
Sposób I

Proste przechodzące przez punkt 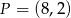P = (8,2) mają równanie postaci

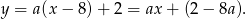
y = a(x− 8)+ 2 = ax + (2 − 8a).

Prosta tej postaci przecina oś 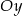Oy w punkcie 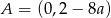A = (0 ,2− 8a ) . Wyznaczmy jeszcze punkt przecięcia z osią Ox .

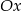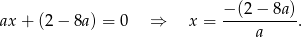
ax + (2 − 8a ) = 0 ⇒ x = −-(2−--8a). a

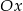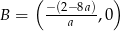W takim razie punkt przecięcia z osią Ox to ( −(2−8a) ) B = ---a---,0 . Jeżeli punkty te mają leżeć na dodatnich półosiach, to musi być ponadto spełniona nierówność 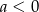a < 0 . Zapisujemy teraz podaną informację o polu trójkąta AOB .

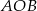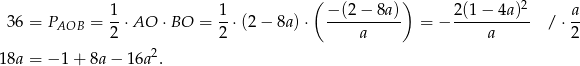
1 1 ( −(2 − 8a )) 2(1 − 4a)2 a 36 = PAOB = --⋅AO ⋅BO = --⋅(2− 8a)⋅ ----------- = − ----------- / ⋅-- 2 2 a a 2 18a = − 1 + 8a − 16a 2.

Rozwiązujemy otrzymane równanie kwadratowe.

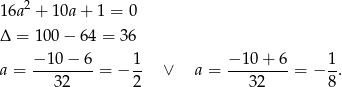
16a2 + 10a + 1 = 0 Δ = 10 0− 64 = 36 a = −-10-−-6-= − 1- ∨ a = −-10+--6-= − 1-. 32 2 32 8

Są zatem dwie proste spełniające warunki zadania.

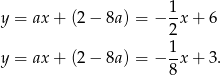
y = ax + (2 − 8a ) = − 1x + 6 2 1- y = ax + (2 − 8a ) = − 8x + 3.

Sposób II

Jeżeli 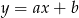y = ax + b jest szukaną prostą, to ponieważ prosta ta przechodzi przez 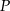P , mamy

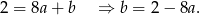
2 = 8a+ b ⇒ b = 2− 8a.

i szukana prosta ma wzór postaci 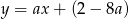y = ax + (2 − 8a) . Dalej zadanie rozwiązujemy tak samo jak w pierwszym sposobie.

Sposób III

Tym razem szukamy prostej w postaci odcinkowej

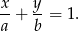
x- y- a + b = 1.

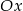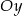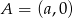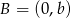Prosta o takim równaniu przecina osie Ox i Oy odpowiednio w punktach A = (a,0) i B = (0,b) . Podane pole trójkąta 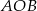AOB daje nam więc równanie

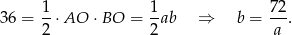
1 1 72 36 = 2-⋅AO ⋅BO = 2ab ⇒ b = a-.

Podstawiając współrzędne punktu 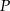P otrzymujemy

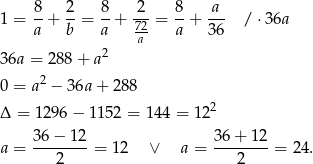
8- 2- 8- 2-- 8- a-- 1 = a + b = a + 72 = a + 36 / ⋅36a a 36a = 288 + a2 2 0 = a − 36a + 288 Δ = 12 96− 1152 = 1 44 = 122 a = 36-−-12-= 12 ∨ a = 36+--12-= 24. 2 2

Mamy wtedy odpowiednio

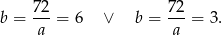
72 72 b = ---= 6 ∨ b = ---= 3 . a a

Są wiec dwie proste spełniające warunki zadania.

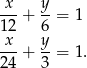
-x- y- 12 + 6 = 1 x y 24-+ 3-= 1.

 
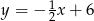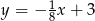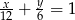Odpowiedź: 1 y = − 2x+ 6 , 1 y = − 8x + 3 , postać odcinkowa: x y 12 + 6 = 1 , x y 24 + 3 = 1

Wersja PDF