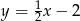Zadanie nr 2102530

Wyznacz równanie prostej prostopadłej do prostej o równaniu 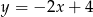y = − 2x + 4 przecinającej oś 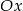w punkcie o odciętej 4.

Rozwiązanie

Zapiszmy równanie szukanej prostej w postaci 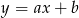y = ax + b . Ponieważ jest ona prostopadła do prostej 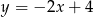y = − 2x + 4 , więc

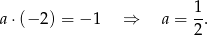
a⋅(− 2) = −1 ⇒ a = 1-. 2

Teraz wykorzystujemy fakt, że prosta przechodzi przez punkt 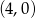(4,0 ) i otrzymujemy

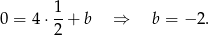
0 = 4 ⋅ 1-+ b ⇒ b = − 2. 2

Zatem szukana prosta ma równanie

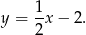
1 y = -x − 2. 2

Na koniec obrazek

Odpowiedź: y = 12x − 2

Nie rozumiesz fragmentu rozwiązania?
W rozwiązaniu jest błąd lub literówka?
Masz inny pomysł na rozwiązanie tego zadania?
Napisz nam o tym!

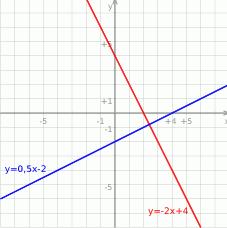
Dodaj komentarz