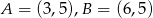Zadanie nr 4367775
Prosta 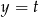 przecina proste
przecina proste 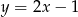 i
i 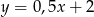 odpowiednio w punktach
odpowiednio w punktach 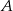 i
i 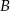 .
.
- Wyraź długość odcinka
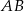 jako funkcję zmiennej
jako funkcję zmiennej 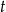 .
. - Wyznacz takie punkty
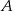 i
i 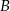 , aby długość odcinka
, aby długość odcinka 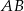 była równa 3.
była równa 3.
Rozwiązanie
Zaczynamy oczywiście od schematycznego rysunku opisanej sytuacji.
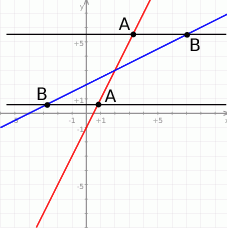
- Aby wyznaczyć współrzędne punktów
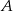 i
i 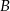 musimy rozwiązać równania
musimy rozwiązać równania 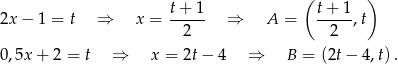
Ponieważ punkty
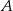 i
i 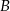 mają takie same drugie współrzędne (leżą na poziomej prostej
mają takie same drugie współrzędne (leżą na poziomej prostej 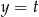 ), więc ich odległość to różnica między ich pierwszymi współrzędnymi. Aby uniknąć problemu z tym, czy punkt
), więc ich odległość to różnica między ich pierwszymi współrzędnymi. Aby uniknąć problemu z tym, czy punkt 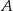 jest na lewo od
jest na lewo od 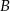 czy na odwrót, wygodnie jest tę odległość zapisać przy pomocy wartości bezwględnej.
czy na odwrót, wygodnie jest tę odległość zapisać przy pomocy wartości bezwględnej. 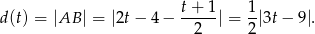
Odpowiedź: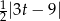
- Musimy rozwiązać równanie
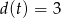 .
. 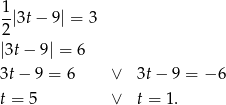
Odpowiedź: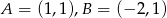 oraz
oraz