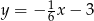/Szkoła średnia/Geometria/Geometria analityczna/Równanie prostej

Zadanie nr 4651877

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz równanie prostej równoległej do prostej 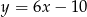y = 6x − 10 przechodzącej przez punkt 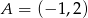A = (− 1,2) oraz równanie prostej prostopadłej do tych prostych przechodzącej przez punkt B = (0,− 3) .

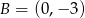Rozwiązanie

Wszystkie proste równoległe do 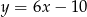y = 6x − 10 są postaci 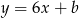y = 6x + b . Współczynnik 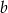b wyznaczamy korzystając z tego, że punkt 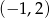(− 1,2) ma być punktem tej prostej:

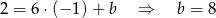
2 = 6 ⋅(− 1) + b ⇒ b = 8

Zatem szukana prosta to 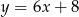y = 6x + 8 .

PIC

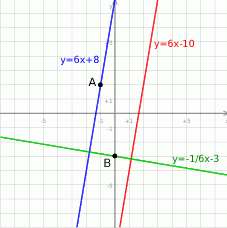
Proste prostopadłe do 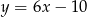y = 6x − 10 są postaci 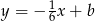y = − 16x + b (iloczyn współczynników kierunkowych musi być równy -1). Współczynnik 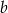b wyznaczamy jak poprzednio:

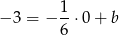
1- − 3 = − 6 ⋅0 + b

Szukana prosta to 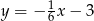y = − 1x − 3 6 .  
Odpowiedź: 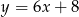y = 6x+ 8 i 1 y = − 6x − 3

Wersja PDF