Zadanie nr 5373821
Punkt 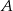 jest punktem wspólnym prostych prostopadłych
jest punktem wspólnym prostych prostopadłych 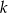 i
i 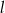 o równaniach
o równaniach 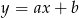 oraz
oraz 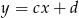 . Wykaż, że jeżeli
. Wykaż, że jeżeli 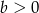 i
i 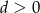 , to druga współrzędna punktu
, to druga współrzędna punktu 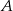 jest liczbą dodatnią.
jest liczbą dodatnią.
Rozwiązanie
Sposób I
Ponieważ proste 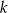 i
i 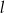 są prostopadłe, to
są prostopadłe, to 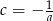 i współrzędne punktu
i współrzędne punktu 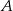 są rozwiązaniami układu równań
są rozwiązaniami układu równań
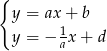
Mnożymy teraz drugie równanie przez 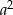 i dodajemy je do pierwszego równania.
i dodajemy je do pierwszego równania.
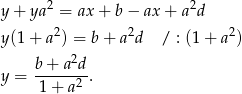
Ponieważ 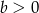 i
i 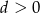 liczba ta jest oczywiście dodatnia.
liczba ta jest oczywiście dodatnia.
Sposób II
Jeżeli 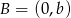 i
i 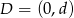 są punktami, w których proste
są punktami, w których proste 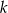 i
i 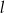 przecinają oś
przecinają oś 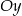 , to trójkąt
, to trójkąt 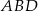 jest trójkątem prostokątnym, którego przeciwprostokątna
jest trójkątem prostokątnym, którego przeciwprostokątna 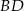 jest zawarta w dodatniej półosi osi
jest zawarta w dodatniej półosi osi 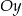 (bo
(bo 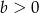 i
i 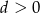 ).
).
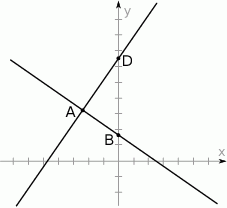
To oznacza, że punkt 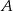 leży pomiędzy prostymi
leży pomiędzy prostymi 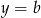 i
i 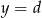 , czyli jego druga współrzędna jest dodatnia.
, czyli jego druga współrzędna jest dodatnia.

