/Szkoła średnia/Geometria/Geometria analityczna/Równanie prostej

Zadanie nr 5387741

Dodaj do ulubionych
Dodaj do rozwiązanych

Wierzchołek kąta znajduje się w punkcie 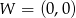W = (0,0) , jedno z jego ramion leży na prostej 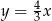y = 43x , a drugie ramię przechodzi przez punkt 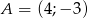A = (4;− 3) . Punkt 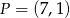P = (7,1) należy do wnętrza tego kąta. Sprawdź rachunkowo, czy punkt 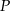P leży na dwusiecznej tego kąta.

Rozwiązanie

Możemy zacząć od szkicowego rysunku.

PIC

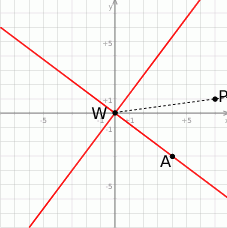
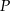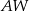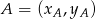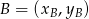Aby sprawdzić czy punkt P leży na dwusiecznej kąta musimy sprawdzić czy jego odległości od tych ramion są równe. Równanie jednego z ramion mamy dane. Równanie drugiego, AW możemy wyliczyć ze wzoru na równanie prostej przechodzącej przez dwa punkty A = (xA ,yA ) i B = (xB,yB ) :

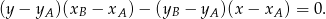
(y− yA)(xB − xA ) − (yB − yA )(x− xA) = 0.

W naszej sytuacji mamy

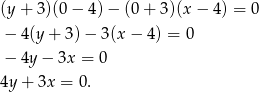
(y + 3)(0 − 4) − (0 + 3)(x − 4) = 0 − 4(y + 3) − 3(x − 4) = 0 − 4y − 3x = 0 4y + 3x = 0.

Równanie to mogliśmy wyprowadzić odrobinę prościej, sprawdzając kiedy prosta 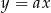y = ax przechodzi przez punkt A .

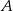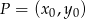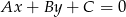Korzystamy teraz ze wzoru na odległość punktu P = (x 0,y 0) od prostej Ax + By + C = 0 :

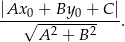
|Ax-0√-+-By-0 +-C|. A 2 + B 2

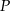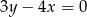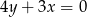Odległości punktu P od ramion kąta, czyli prostych 3y − 4x = 0 i 4y + 3x = 0 wynoszą

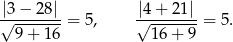
|√3-−-28|-= 5, |√4+--21|-= 5. 9 + 16 16+ 9

 
Odpowiedź: Tak, punkt ten leży na dwusiecznej kąta.

Wersja PDF