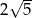/Szkoła średnia/Geometria/Geometria analityczna/Równanie prostej

Zadanie nr 5466106

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz odległość między prostymi 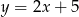y = 2x + 5 i y = 2x − 5 .

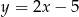Rozwiązanie

Rozpoczynamy od szkicowego rysunku.

PIC

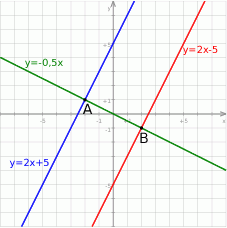
Sposób I

Odległość między prostymi obliczymy w następujący sposób: napiszemy równanie prostej prostopadłej do danych prostych i znajdziemy jej punkty przecięcia 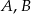A ,B z tymi prostymi. Odległość między prostymi będzie równa długości odcinka AB .

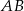Jako prostą prostopadłą do danych prostych możemy wziąć 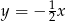1 y = − 2 x (możemy też wziąć jakąkolwiek inną ze współczynnikiem kierunkowym 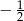− 12 , nie ma to większego znaczenia). Szukamy jej punktów wspólnych z danymi prostymi.

Najpierw z pierwszą prostą

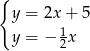
{ y = 2x + 5 y = − 1x 2

Porównujemy 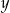y -ki.

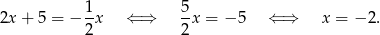
1- 5- 2x + 5 = − 2x ⇐ ⇒ 2x = −5 ⇐ ⇒ x = − 2.

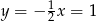Stąd y = − 1x = 1 2 i A = (− 2,1) .

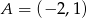Teraz punkt wspólny z drugą prostą

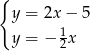
{ y = 2x − 5 y = − 12x

Porównujemy 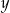y -ki.

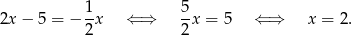
1- 5- 2x − 5 = − 2x ⇐ ⇒ 2x = 5 ⇐ ⇒ x = 2.

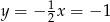Stąd y = − 1x = − 1 2 i B = (2,− 1) .

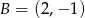Pozostało obliczyć długość odcinka 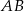AB .

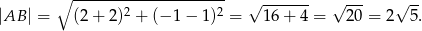
∘ --------------------- 2 2 √ ------- √ --- √ -- |AB | = (2 + 2) + (− 1 − 1) = 16 + 4 = 20 = 2 5.

Sposób II

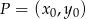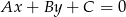Skorzystamy ze wzoru na odległość punktu P = (x 0,y 0) od prostej Ax + By + C = 0 :

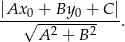
|Ax-0√-+-By-0 +-C|. A 2 + B 2

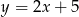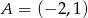W naszej sytuacji za punkt możemy wziąć dowolny punkt prostej y = 2x + 5 , np. A = (− 2,1) , a za prostą: prostą 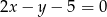2x − y− 5 = 0 . Szukana odległość jest więc równa

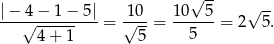
√ -- |− 4− 1− 5| 10 10 5 √ -- ---√----------= √---= ------= 2 5. 4 + 1 5 5

 
Odpowiedź: √ -- 2 5

Wersja PDF