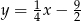/Szkoła średnia/Geometria/Geometria analityczna/Równanie prostej

Zadanie nr 5591594

Dodaj do ulubionych
Dodaj do rozwiązanych

Dana jest funkcja 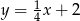1 y = 4x + 2 . Podaj równanie prostej prostopadłej i prostej równoległej do danej prostej, do których należy punkt 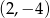(2 ,−4 ) . Wykonaj rysunek do zadania.

Rozwiązanie

Rozpoczynamy od szkicowego rysunku.

PIC

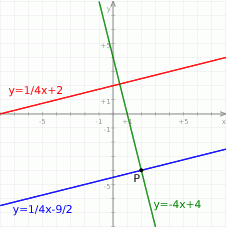
Prosta równoległa do danej prostej musi mieć postać 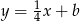y = 14 x+ b . Współczynnik 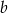b wyznaczamy podstawiając współrzędne punktu P = (2,− 4) .

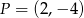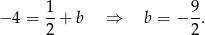
1- 9- − 4 = 2 + b ⇒ b = − 2 .

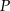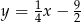Zatem prosta równoległa do danej prostej i przechodząca przez punkt P ma równanie y = 1x − 9 4 2 .

Prosta prostopadła do danej prostej musi mieć postać 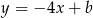y = − 4x + b . Współczynnik 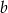b wyznaczamy podstawiając współrzędne punktu P = (2,− 4) .

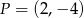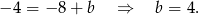
− 4 = −8 + b ⇒ b = 4.

Zatem prosta prostopadła do danej prostej i przechodząca przez punkt 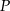P ma równanie y = − 4x + 4 .  
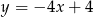Odpowiedź: 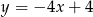y = −4x + 4 i y = 1x − 9 4 2

Wersja PDF