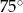Zadanie nr 6241130
Oblicz miarę kąta ostrego, którego ramiona są zawarte w prostych o równaniach 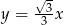 i
i 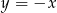 .
.
Rozwiązanie
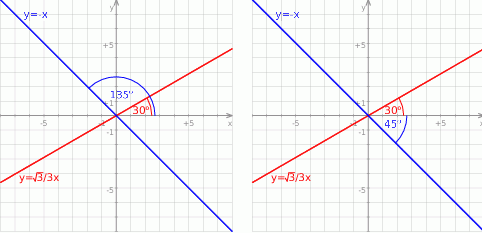
Szkicujemy podane proste w układzie współrzędnych.
Sposób I
Prosta 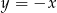 tworzy z dodatnią półosią
tworzy z dodatnią półosią 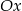 układu współrzędnych kąt, którego tangens jest równy
układu współrzędnych kąt, którego tangens jest równy 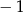 (współczynnik kierunkowy tej prostej), czyli
(współczynnik kierunkowy tej prostej), czyli 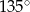 . Podobnie, prosta
. Podobnie, prosta 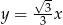 tworzy z dodatnią półosią
tworzy z dodatnią półosią 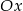 układu współrzędnych kąt, którego tangens jest równy
układu współrzędnych kąt, którego tangens jest równy 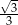 (współczynnik kierunkowy tej prostej), czyli
(współczynnik kierunkowy tej prostej), czyli 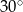 . To oznacza, że proste przecinają się pod kątem
. To oznacza, że proste przecinają się pod kątem
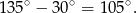
To jest jednak kąt rozwarty, kąt ostry utworzony przez proste, to
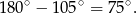
Sposób II
Tak jak poprzednio stwierdzamy, że prosta 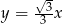 tworzy z dodatnią półosią
tworzy z dodatnią półosią 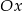 kąt
kąt 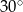 . Prosta
. Prosta 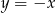 jest dwusieczną kąta utworzonego przez osie układu, więc tworzy kąt ostry z osiami równy
jest dwusieczną kąta utworzonego przez osie układu, więc tworzy kąt ostry z osiami równy 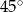 . To oznacza (patrzymy na prawy rysunek), że kąt ostry między danymi prostymi jest równy
. To oznacza (patrzymy na prawy rysunek), że kąt ostry między danymi prostymi jest równy
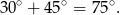
Odpowiedź: