Zadanie nr 6357687
W układzie współrzędnych są dane punkty 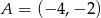 ,
, 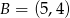 .
.
- Oblicz odległość punktu
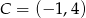 od prostej przechodzącej przez punkty
od prostej przechodzącej przez punkty 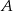 i
i 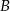 .
. - Uzasadnij, że jeśli
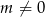 , to punkty
, to punkty 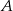 ,
, 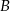 oraz punkt
oraz punkt 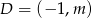 są wierzchołkami trójkąta.
są wierzchołkami trójkąta.
Rozwiązanie
- Zacznijmy od rysunku.
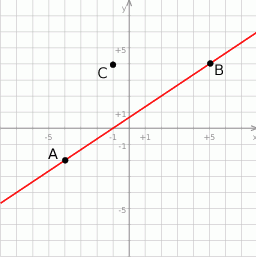
Aby móc skorzystać ze wzoru na odległość punktu od prostej musimy mieć równanie prostej
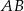 . Korzystamy ze wzoru na równanie prostej przez dwa punkty
. Korzystamy ze wzoru na równanie prostej przez dwa punkty 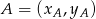 i
i 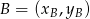 :
: 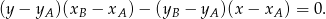
W naszej sytuacji:
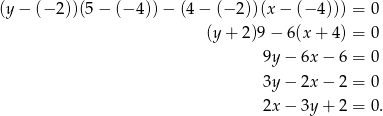
Teraz korzystamy ze wzoru na odległość punktu
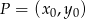 od prostej
od prostej 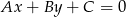 :
: 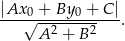
W naszej sytuacji mamy:
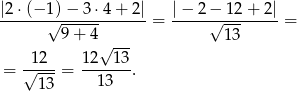
Odpowiedź: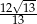
- Co to znaczy, że 3 punkty są wierzchołkami trójkąta? – to znaczy, że nie leżą na jednej prostej. Musimy zatem sprawdzić, że punkt
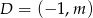 nie leży na prostej
nie leży na prostej 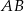 . Ponieważ wyliczyliśmy już równanie tej prostej, nie ma z tym problemu (wstawiamy współrzędne tego punktu do równania prostej i patrzymy, że nie wyjdzie 0):
. Ponieważ wyliczyliśmy już równanie tej prostej, nie ma z tym problemu (wstawiamy współrzędne tego punktu do równania prostej i patrzymy, że nie wyjdzie 0):