Zadanie nr 7220105
Sprawdź czy proste  i
i 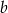 są równoległe, jeśli prosta
są równoległe, jeśli prosta  przecina oś
przecina oś  w punkcie
w punkcie 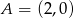 , oś
, oś 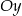 w punkcie
w punkcie 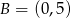 , a prosta
, a prosta 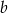 przecina oś
przecina oś 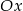 w punkcie
w punkcie 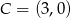 i oś
i oś 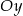 w punkcie
w punkcie 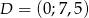 .
.
Rozwiązanie
Sposób I
Z podanych informacji o punktach przecięcia z osią 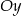 mamy równania prostych
mamy równania prostych
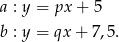
Współczynniki 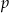 i
i 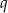 wyznaczamy z punktów przecięcia z osią
wyznaczamy z punktów przecięcia z osią 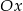 .
.
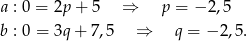
Ponieważ współczynniki kierunkowe są takie same, proste są równoległe.
Sposób II
Wystarczy sprawdzić czy wektory 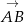 i
i 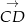 są równoległe. Liczymy
są równoległe. Liczymy
![→ AB = [− 2,5] → CD = [− 3,7 ,5 ].](https://img.zadania.info/zad/7220105/HzadR8x.gif)
Łatwo sprawdzić, że współrzędne wektorów są proporcjonalne:
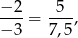
więc wektory są równoległe.
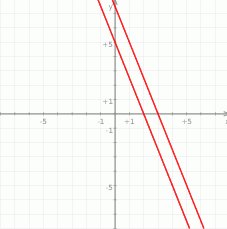
Odpowiedź: Tak, są równoległe.

