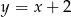/Szkoła średnia/Geometria/Geometria analityczna/Równanie prostej

Zadanie nr 7665209

Dodaj do ulubionych
Dodaj do rozwiązanych

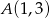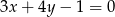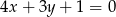Wykaż, że punkt A (1,3) leży na dwusiecznej kąta między prostymi 3x + 4y − 1 = 0 i 4x + 3y + 1 = 0 . Napisz równanie tej dwusiecznej.

Rozwiązanie

Zaczynamy od szkicowego rysunku.

PIC

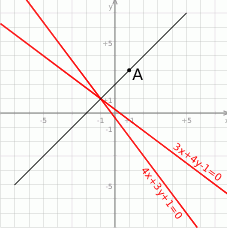
Punkty leżące na dwusiecznej kąta to punkty, które są równo odległe od jego ramion. Ponieważ i tak musimy wyznaczyć równanie dwusiecznej, zaczniemy od tego, a na końcu sprawdzimy, że leży na niej dany punkt. Na mocy wzoru na odległość punktu od prostej punkty na dwusiecznej muszą spełniać równanie.

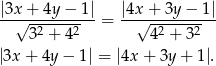
|3x + 4y − 1| |4x+ 3y− 1| --√---------- = --√---------- 32 + 42 42 + 32 |3x + 4y − 1| = |4x + 3y + 1|.

Teraz dochodzimy do najtrudniejszego momentu, musimy opuścić wartości bezwzględne. Z jakim znakiem? To zależy od tego, o którą dwusieczną nam chodzi (są dwie). Dwusieczna przechodząca przez punkt 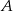A leży całkowicie powyżej, albo całkowicie poniżej obu danych prostych, dlatego oba wyrażenia pod wartością bezwzględną mają na niej ten sam znak. Zatem opuszczamy wartości bezwzględne nie zmieniając znaku (mogliśmy też rozważyć dwa przypadki, a potem wybrać dwusieczną, o którą nam chodzi).

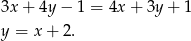
3x + 4y − 1 = 4x+ 3y + 1 y = x + 2.

Teraz widać gołym okiem, że punkt 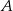A leży na tej prostej.  
Odpowiedź: y = x+ 2

Wersja PDF