/Szkoła średnia/Geometria/Geometria analityczna/Równanie prostej

Zadanie nr 7764405

Dodaj do ulubionych
Dodaj do rozwiązanych

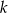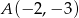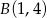Prosta k przechodzi przez punkty A (− 2,− 3) i B(1,4) . Wyznacz równania prostej 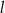l prostopadłej do 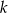k i prostej 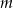m równoległej do 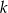k , jeżeli każda z nich przechodzi przez punkt C (2,− 1) .

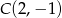Rozwiązanie

Zaczynamy od szkicowego rysunku.

PIC

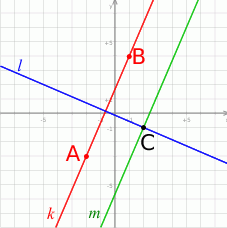
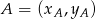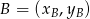Korzystamy ze wzoru na równanie prostej przechodzącej przez dwa punkty A = (xA ,yA ) i B = (xB ,yB) :

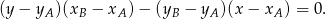
(y− yA)(xB − xA ) − (yB − yA )(x− xA) = 0.

W naszej sytuacji mamy

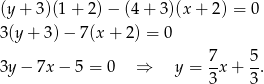
(y + 3)(1 + 2)− (4+ 3)(x + 2) = 0 3(y + 3) − 7(x + 2) = 0 7- 5- 3y − 7x − 5 = 0 ⇒ y = 3 x + 3.

Prosta prostopadła do 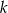k ma postać 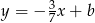y = − 37x + b . Współczynnik 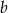b wyznaczamy z podanego punktu 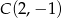C(2,− 1) tej prostej.

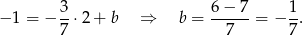
3- 6-−-7- 1- − 1 = − 7 ⋅2 + b ⇒ b = 7 = − 7.

Zatem prosta 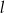l ma rownanie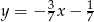 y = − 37x− 17

Prosta 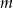m jest postaci 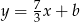y = 7x + b 3 . Jak poprzednio, współczynnik 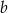b wyznaczamy z podanego punktu C(2,− 1) .

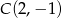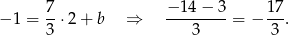
7 − 14 − 3 17 − 1 = -⋅ 2+ b ⇒ ---------= − --. 3 3 3

Zatem 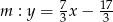7 17- m : y = 3x − 3  
Odpowiedź: 3 1 7 17 l : y = − 7x − 7, m : y = 3x− 3-

Wersja PDF