Zadanie nr 7838063
Dany jest ciąg 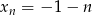 dla
dla 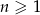 . Ciąg
. Ciąg 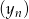 ma tę własność, że dla każdego
ma tę własność, że dla każdego 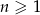 punkty o współrzędnych
punkty o współrzędnych 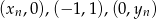 leżą na jednej prostej. Wyznacz wzór ogólny ciągu
leżą na jednej prostej. Wyznacz wzór ogólny ciągu 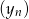 .
.
Rozwiązanie
Największa trudność w tym zadaniu, to makabryczne sformułowanie. Pełno dziwnych znaczków i trudno się połapać o co chodzi. No więc trochę to uprośćmy. Po pierwsze, oznaczenie ciągu 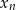 jest zupełnie niepotrzebne, można ciąg
jest zupełnie niepotrzebne, można ciąg 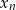 wywalić i warunek z zadania zastąpić warunkiem: punkty
wywalić i warunek z zadania zastąpić warunkiem: punkty 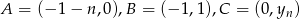 leżą na jednej prostej. Ok, nie ma już ciągu
leżą na jednej prostej. Ok, nie ma już ciągu 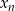 .
.
Kolejna myśl, to jak to jest, że fakt, że punkt 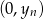 leży na prostej wyznaczonej przez
leży na prostej wyznaczonej przez 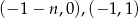 pozwala wyliczyć
pozwala wyliczyć 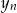 ? - przecież na tej prostej jest pełno punktów. Żeby to zrozumieć, trzeba zrobić rysunek.
? - przecież na tej prostej jest pełno punktów. Żeby to zrozumieć, trzeba zrobić rysunek.
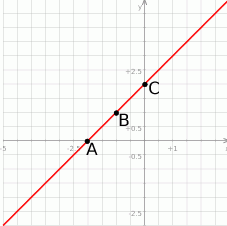
Na tym schematycznym rysunku zaznaczone są przykładowe punkty i prosta. Punkt 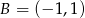 stoi w miejscu, punkt
stoi w miejscu, punkt 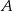 (na osi
(na osi 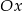 ) zmienia się (w zależności od
) zmienia się (w zależności od  ), a punkt
), a punkt 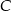 (na osi
(na osi 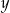 ) to ten którego szukamy.
) to ten którego szukamy.
Po tym wstępie wszystko powinno być jasne.
Sposób I
Piszemy wektory 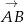 i
i 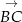 i sprawdzamy kiedy są równoległe.
i sprawdzamy kiedy są równoległe.
![→ AB = [n,1] → BC = [1,yn − 1].](https://img.zadania.info/zad/7838063/HzadR16x.gif)
Wektory ![[x1,y1]](https://img.zadania.info/zad/7838063/HzadR17x.gif) i
i ![[x2,y2]](https://img.zadania.info/zad/7838063/HzadR18x.gif) są równoległe wtedy i tylko wtedy gdy
są równoległe wtedy i tylko wtedy gdy 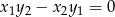 (równoważnie, współrzędne są proporcjonalne). Otrzymujemy zatem równanie
(równoważnie, współrzędne są proporcjonalne). Otrzymujemy zatem równanie
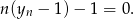
Stąd 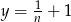 .
.
Sposób II
Załóżmy, że prosta na której leżą punkty 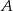 i
i 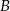 ma równanie
ma równanie 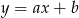 . Otrzymujemy stąd układ równań
. Otrzymujemy stąd układ równań
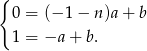
Chcemy z tego układu wyliczyć 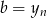 . W tym celu mnożymy drugie przez
. W tym celu mnożymy drugie przez 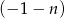 i dodajemy do pierwszego (żeby skrócić
i dodajemy do pierwszego (żeby skrócić  ):
):
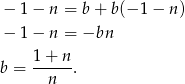
Odpowiedź: