/Szkoła średnia/Geometria/Geometria analityczna/Równanie prostej

Zadanie nr 8014241

Dodaj do ulubionych
Dodaj do rozwiązanych

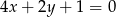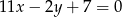Znaleźć równania dwusiecznych kątów wyznaczonych przez proste o równaniach 4x + 2y + 1 = 0 i 11x − 2y + 7 = 0 .

Rozwiązanie

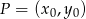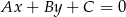Korzystamy ze wzoru na odległość punktu P = (x0,y0) od prostej Ax + By + C = 0 :

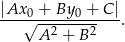
|Ax-0√-+-By-0 +-C|. A 2 + B 2

Dwusieczna to zbiór punktów równo odległych od obu prostych czyli zbiór punktów postaci

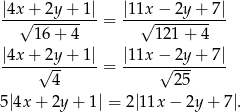
|4x-+--2y+--1| |11x-−-2y-+-7-| √ 16-+-4- = √ 121+--4- |4x-+-√2y+--1|= |11x-−√-2y-+-7-| 4 25 5 |4x + 2y+ 1| = 2|11x − 2y + 7|.

Zbiór opisany tym równaniem to tak naprawdę obie dwusieczne. Jeżeli chcemy je rozdzielić to musimy opuścić wartości bezwzględne. Możemy to zrobić na dwa sposoby (wybór znaków), to da nam równania dwusiecznych.

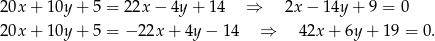
20x + 10y + 5 = 22x − 4y+ 14 ⇒ 2x − 14y + 9 = 0 20x + 10y + 5 = − 22x + 4y − 14 ⇒ 42x + 6y + 19 = 0.

Na koniec rysunek całej sytuacji.

PIC

 
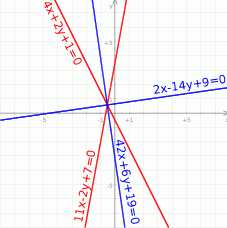
Odpowiedź: 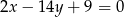2x − 14y+ 9 = 0 i 42x + 6y+ 19 = 0

Wersja PDF