Zadanie nr 9210511
Dany jest punkt 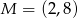 . Wyznacz równanie takiej prostej
. Wyznacz równanie takiej prostej 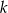 , do której należy punkt
, do której należy punkt 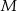 , że na ujemnej półosi
, że na ujemnej półosi 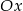 i dodatniej półosi
i dodatniej półosi 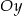 układu
układu 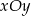 prosta ta wyznacza odcinki
prosta ta wyznacza odcinki 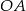 i
i 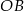 , których suma długości jest równa 6. Oblicz obwód trójkąta
, których suma długości jest równa 6. Oblicz obwód trójkąta 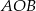 .
.
Rozwiązanie
Zacznijmy od rysunku.
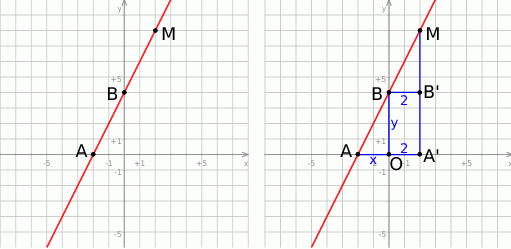
Sposób I
Jeżeli 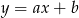 jest szukaną prostą, to ponieważ prosta ta przechodzi przez
jest szukaną prostą, to ponieważ prosta ta przechodzi przez 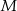 , mamy
, mamy
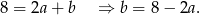
Aby wyznaczyć  liczymy w jakich punktach prosta ta, czyli
liczymy w jakich punktach prosta ta, czyli 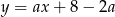 przecina osie
przecina osie 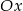 i
i 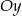 . Oś
. Oś 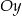 przecina w punkcie
przecina w punkcie 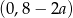 . Musimy mieć zatem
. Musimy mieć zatem
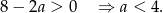
Aby znaleźć punkt przcięcia z osią 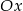 rozwiązujemy równanie
rozwiązujemy równanie
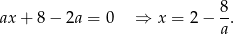
Musimy zatem mieć
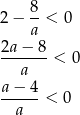
Ponieważ już wcześniej ustaliliśmy, że 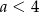 , nierówność ta oznacza, że
, nierówność ta oznacza, że 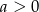 , czyli
, czyli
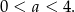
Zapiszmy teraz warunek 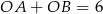 .
.
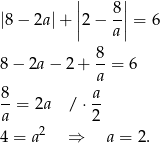
Mamy zatem 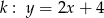 ,
, 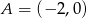 i
i 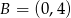 . Ponieważ trójkąt
. Ponieważ trójkąt 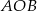 jest prostokątny, to
jest prostokątny, to
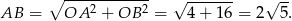
Tak więc obwód trójkąta jest równy
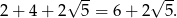
Sposób II
Jeżeli 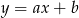 jest szukaną prostą, to przecina ona oś
jest szukaną prostą, to przecina ona oś 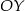 w punkcie
w punkcie 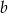 i oś
i oś 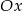 w punkcie
w punkcie 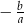 . Musimy zatem założyć, że
. Musimy zatem założyć, że 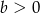 i
i 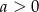 . Warunek
. Warunek 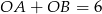 prowadzi do równania
prowadzi do równania
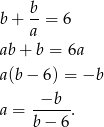
Pozostało sprawdzić, kiedy punkt 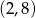 jest na prostej
jest na prostej 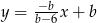 .
.
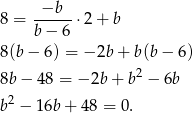
Liczymy dalej, 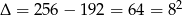 ,
, 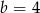 lub
lub 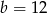 . Druga z tych liczb daje jednak
. Druga z tych liczb daje jednak 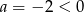 , co jest sprzeczne z naszymi założeniami. Zatem
, co jest sprzeczne z naszymi założeniami. Zatem 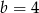 i
i 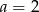 . Obwód trójkąta
. Obwód trójkąta 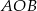 wyliczamy jak w sposobie I.
wyliczamy jak w sposobie I.
Sposób III
Poprowadźmy pionową prostą przez punkt 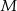 (prawy rysunek). Przy oznaczeniach z rysunku, trójkąty
(prawy rysunek). Przy oznaczeniach z rysunku, trójkąty 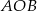 i
i 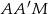 są podobne, więc
są podobne, więc
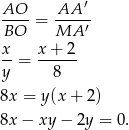
Wiemy ponadto, że 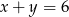 . Podstawmy
. Podstawmy 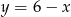 w powyższym równaniu.
w powyższym równaniu.
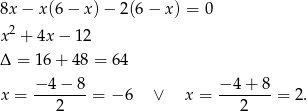
Ujemne rozwiązanie odrzucamy (jest sprzeczne z naszym rysunkiem) i mamy 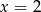 . W takim razie
. W takim razie 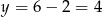 i szukana prosta ma równanie
i szukana prosta ma równanie
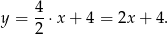
Mamy ponadto 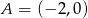 ,
, 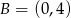 . Obwód liczymy jak w poprzednich sposobach.
. Obwód liczymy jak w poprzednich sposobach.
Odpowiedź: 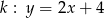 , Obwód:
, Obwód: 

