/Szkoła średnia/Geometria/Geometria analityczna/Równanie prostej

Zadanie nr 9917203

Dodaj do ulubionych
Dodaj do rozwiązanych

W układzie współrzędnych dane są dwa punkty: 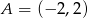A = (− 2,2) i B = (4,4) .

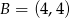  • Wyznacz równanie symetralnej odcinka AB .
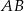  • Prosta 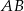AB oraz prosta o równaniu 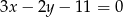3x − 2y − 1 1 = 0 przecinają się w punkcie 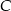C . Oblicz współrzędne punktu C .

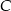Rozwiązanie

Zaczynamy od szkicowego rysunku.

PIC

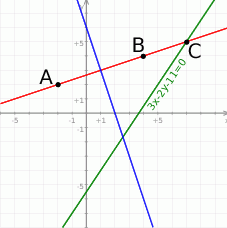
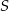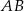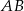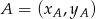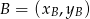  • Szukana symetralna to prosta przechodząca przez środek S odcinka AB i do niego prostopadła. Zacznijmy od napisania równania prostej AB . Korzystamy ze wzoru na równanie prostej przechodzącej przez dwa punkty A = (xA ,yA) i B = (xB,yB ) :
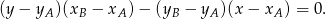
    (y − yA )(xB − xA )− (yB − yA)(x − xA ) = 0.

    W naszej sytuacji mamy

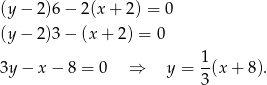
    (y − 2)6 − 2(x + 2) = 0 (y − 2)3 − (x + 2 ) = 0 3y − x − 8 = 0 ⇒ y = 1(x + 8). 3

    Szukana symetralna ma zatem współczynnik kierunkowy 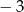− 3 (bo jest prostopadła do 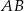AB ), czyli jest postaci 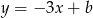y = − 3x+ b . Współczynnik 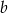b wyznaczymy korzystając z tego, że symetralna przechodzi przez środek odcinka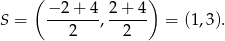

    ( ) −-2+-4- 2-+-4- S = 2 , 2 = (1,3).

    Mamy zatem

    3 = − 3 + b ⇒ b = 6.

     
    Odpowiedź: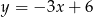 y = − 3x + 6

  • W poprzednim podpunkcie wyznaczyliśmy równanie prostej 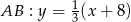AB : y = 1(x + 8) 3 . Podstawiamy tę wartość do podanego równania prostej.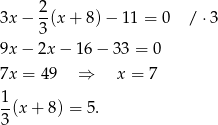
    2 3x− -(x + 8 )− 1 1 = 0 / ⋅3 3 9x− 2x − 16 − 33 = 0 7x = 49 ⇒ x = 7 1(x + 8) = 5. 3

     
    Odpowiedź: C = (7,5)

Wersja PDF