/Szkoła średnia/Zadania maturalne/Matura 2015
Egzamin Maturalny
z Matematyki poziom rozszerzony 8 maja 2015 Czas pracy: 180 minut
Zadania zamknięte
Na rysunku przedstawiony jest zbiór wszystkich liczb rzeczywistych spełniających nierówność 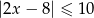 .
.
![]()
Stąd wynika, że
A) 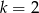 B)
B) 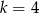 C)
C) 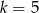 D)
D) 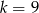
Dana jest funkcja 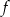 określona wzorem
określona wzorem 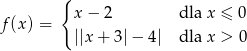
Równanie 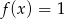 ma dokładnie
ma dokładnie
A) jedno rozwiązanie. B) dwa rozwiązania. C) cztery rozwiązania. D) pięć rozwiązań.
Liczba 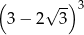 jest równa
jest równa
A) 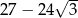 B)
B) 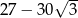 C)
C) 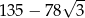 D)
D) 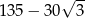
Równanie 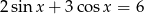 w przedziale
w przedziale 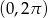
A) nie ma rozwiązań rzeczywistych.
B) ma dokładnie jedno rozwiązanie rzeczywiste.
C) ma dokładnie dwa rozwiązania rzeczywiste.
D) ma więcej niż dwa rozwiązania rzeczywiste.
Odległość początku układu współrzędnych od prostej o równaniu 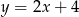 jest równa
jest równa
A) 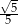 B)
B) 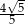 C)
C)  D) 4
D) 4
Zadania otwarte
Oblicz granicę 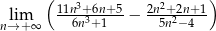 .
.
Liczby 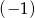 i 3 są miejscami zerowymi funkcji kwadratowej
i 3 są miejscami zerowymi funkcji kwadratowej 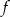 . Oblicz
. Oblicz 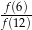 .
.
Udowodnij, że dla każdej liczby rzeczywistej  prawdziwa jest nierówność
prawdziwa jest nierówność
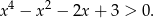
Dwusieczne czworokąta 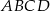 wpisanego w okrąg przecinają się w czterech różnych punktach:
wpisanego w okrąg przecinają się w czterech różnych punktach: 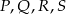 (zobacz rysunek).
(zobacz rysunek).
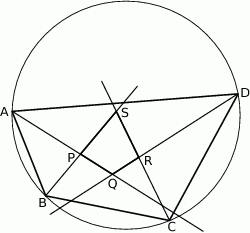
Wykaż, że na czworokącie  można opisać okrąg.
można opisać okrąg.
Długości boków czworokąta 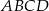 są równe:
są równe: 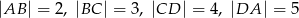 . Na czworokącie
. Na czworokącie 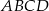 opisano okrąg. Oblicz długość przekątnej
opisano okrąg. Oblicz długość przekątnej 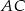 tego czworokąta.
tego czworokąta.
W pierwszej urnie umieszczono 3 kule białe i 5 kul czarnych, a w drugiej urnie 7 kul białych i 2 kule czarne. Losujemy jedną kulę z pierwszej urny, przekładamy ją do urny drugiej i dodatkowo dokładamy do urny drugiej jeszcze dwie kule tego samego koloru, co wylosowana kula. Następnie losujemy dwie kule z urny drugiej. Oblicz prawdopodobieństwo zdarzenia polegającego na tym, że obie kule wylosowane z drugiej urny będą białe.
Funkcja 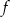 określona jest wzorem
określona jest wzorem 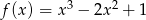 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wyznacz równania tych stycznych do wykresu funkcji
. Wyznacz równania tych stycznych do wykresu funkcji 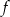 , które są równoległe do prostej o równaniu
, które są równoległe do prostej o równaniu 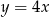 .
.
Dany jest trójmian kwadratowy 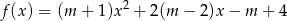 . Wyznacz wszystkie wartości parametru
. Wyznacz wszystkie wartości parametru 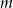 , dla których trójmian
, dla których trójmian 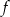 ma dwa różne pierwiastki rzeczywiste
ma dwa różne pierwiastki rzeczywiste 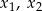 , spełniające warunek
, spełniające warunek 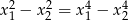 .
.
Podstawą ostrosłupa 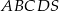 jest kwadrat
jest kwadrat 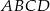 . Krawędź boczna
. Krawędź boczna 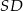 jest wysokością ostrosłupa, a jej długość jest dwa razy większa od długości krawędzi podstawy. Oblicz sinus kąta między ścianami bocznymi
jest wysokością ostrosłupa, a jej długość jest dwa razy większa od długości krawędzi podstawy. Oblicz sinus kąta między ścianami bocznymi 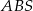 i
i 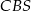 tego ostrosłupa.
tego ostrosłupa.
Suma wszystkich czterech współczynników wielomianu 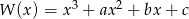 jest równa 0. Trzy pierwiastki tego wielomianu tworzą ciąg arytmetyczny o różnicy równej 3. Oblicz współczynniki
jest równa 0. Trzy pierwiastki tego wielomianu tworzą ciąg arytmetyczny o różnicy równej 3. Oblicz współczynniki 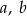 i
i  . Rozważ wszystkie możliwe przypadki.
. Rozważ wszystkie możliwe przypadki.
Rozpatrujemy wszystkie stożki, których przekrojem osiowym jest trójkąt o obwodzie 20. Oblicz wysokość i promień podstawy tego stożka, którego objętość jest największa. Oblicz objętość tego stożka.

