/Szkoła średnia/Zadania maturalne/Matura 2015
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy
(technikum) 28 lutego 2015 Czas pracy: 170 minut
Zadania zamknięte
Wynikiem działania 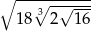 jest
jest
A) 36 B) 16 C) 12 D) 6
Narty kosztowały 680 zł. O ile procent należałoby obniżyć cenę nart, aby kosztowały 595 zł?
A) 8,5% B) 12,5% C) 14,2% D) 25%
Suma przedziałów 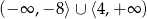 jest zbiorem rozwiązań nierówności
jest zbiorem rozwiązań nierówności
A) 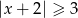 B)
B) 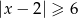 C)
C) 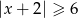 D)
D) 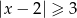
Nierówność 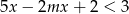 jest spełniona przez każdą liczbę rzeczywistą jeżeli
jest spełniona przez każdą liczbę rzeczywistą jeżeli
A) 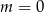 B)
B) 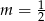 C)
C) 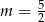 D)
D) 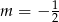
Jeżeli 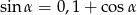 to liczba
to liczba 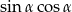 jest równa
jest równa
A) 0,5 B) 0,495 C) 0,99 D) 0,45
Ile rozwiązań ma układ równań 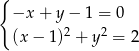 ?
?
A) 0 B) 1 C) 2 D) 3
Dla każdej liczby rzeczywistej  , wyrażenie
, wyrażenie 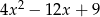 jest równe
jest równe
A) 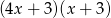 B)
B) 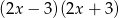 C)
C) 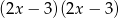 D)
D) 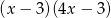
Na tablicy wypisano kolejne wyrazy pewnego ciągu arytmetycznego
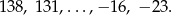
Ile liczb napisano na tablicy?
A) 21 B) 22 C) 23 D) 24
Wyrażenie 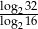 ma wartość równą
ma wartość równą
A) 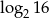 B)
B) 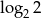 C)
C)  D) 2
D) 2
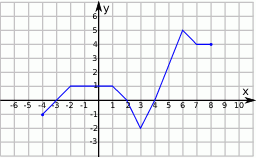
Korzystając z danego wykresu funkcji 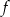 , wskaż nierówność prawdziwą
, wskaż nierówność prawdziwą
A) 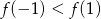 B)
B) 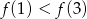 C)
C) 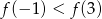 D)
D) 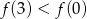
Punkty 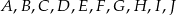 dzielą okrąg o środku
dzielą okrąg o środku 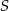 na dziesięć równych łuków. Oblicz miarę kąta
na dziesięć równych łuków. Oblicz miarę kąta 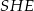 zaznaczonego na rysunku.
zaznaczonego na rysunku.
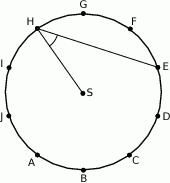
A) 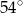 B)
B) 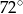 C)
C) 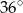 D)
D) 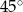
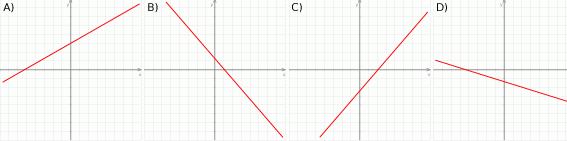
Na którym rysunku przedstawiono wykres funkcji liniowej 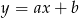 takiej, że
takiej, że 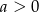 i
i 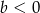 ?
?
Liczby 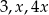 są odpowiednio pierwszym, trzecim i piątym wyrazem ciągu geometrycznego. Wtedy
są odpowiednio pierwszym, trzecim i piątym wyrazem ciągu geometrycznego. Wtedy
A) 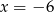 B)
B) 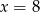 C)
C) 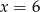 D)
D) 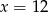
Prostokąt 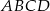 o przekątnej długości
o przekątnej długości 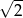 jest podobny do prostokąta o bokach długości 1 i 7. Obwód prostokąta
jest podobny do prostokąta o bokach długości 1 i 7. Obwód prostokąta 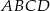 jest równy
jest równy
A) 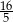 B)
B) 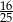 C) 80 D) 16
C) 80 D) 16
Wartość wyrażenia 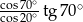 wynosi
wynosi
A) 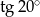 B)
B) 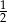 C) 1 D)
C) 1 D) 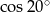
Prosta 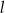 ma równanie
ma równanie 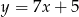 . Równanie prostej prostopadłej do
. Równanie prostej prostopadłej do 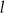 i przechodzącej przez punkt
i przechodzącej przez punkt 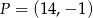 ma postać
ma postać
A) 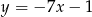 B)
B) 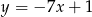 C)
C) 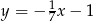 D)
D) 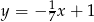
Do okręgu o środku 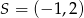 i promieniu
i promieniu 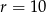 należy punkt o współrzędnych
należy punkt o współrzędnych
A) 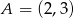 B)
B) 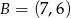 C)
C) 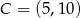 D)
D) 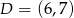
Cięciwa okręgu ma długość 24 cm i jest oddalona od jego środka o 5 cm. Promień tego okręgu ma długość
A) 13 cm B) 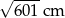 C) 5 cm D)
C) 5 cm D) 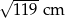
Każdą krawędź graniastosłupa prostego o podstawie będącej sześciokątem skrócono dwukrotnie. W wyniku tej zmiany pole powierzchni graniastosłupa zmniejszyło się o
A) 25% B) 50% C) 75% D) 100%
Rzucając wielokrotnie symetryczną kostką do gry otrzymano następujące liczby oczek
| Liczba oczek | 1 | 2 | 3 | 4 | 5 | 6 |
| Liczba wyników | 5 | 3 | 4 | 1 | 5 | 2 |
Średnia liczba oczek otrzymana w jednym rzucie jest równa.
A) 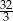 B) 3,5 C) 3,2 D)
B) 3,5 C) 3,2 D) 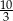
Liczba wszystkich krawędzi graniastosłupa jest o 10 większa od liczby wszystkich jego ścian bocznych. Stąd wynika, że podstawą tego graniastosłupa jest
A) czworokąt B) pięciokąt C) sześciokąt D) dziesięciokąt
Na rysunku przedstawione są wykresy funkcji 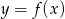 oraz
oraz 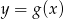 .
.
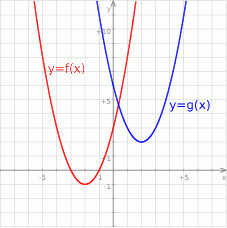
Wówczas :
A) 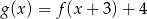
B) 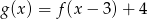
C) 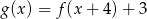
D) 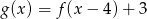
Wiadomo, że mediana liczb 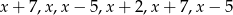 jest równa średniej tych liczb. Zatem liczba
jest równa średniej tych liczb. Zatem liczba 
A) jest równa 3 B) jest równa 4 C) jest równa 5 D) może mieć dowolną wartość
Prawdopodobieństwo zdarzenia 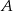 jest 3 razy mniejsze niż prawdopodobieństwo zdarzenia przeciwnego do
jest 3 razy mniejsze niż prawdopodobieństwo zdarzenia przeciwnego do 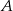 . Wobec tego prawdopodobieństwo zdarzenia
. Wobec tego prawdopodobieństwo zdarzenia 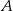 jest równe
jest równe
A) 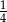 B)
B) 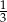 C)
C) 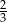 D)
D) 
Zadania otwarte
Rozwiąż nierówność 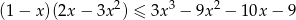 .
.
Wyznacz sumę wszystkich dwucyfrowych parzystych liczb naturalnych.
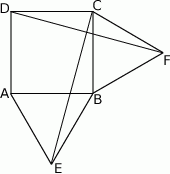
Na zewnątrz kwadratu 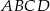 na bokach
na bokach 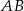 i
i 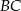 zbudowano trójkąty równoboczne
zbudowano trójkąty równoboczne 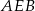 i
i 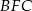 . Uzasadnij, że proste
. Uzasadnij, że proste 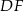 i
i 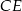 są prostopadłe.
są prostopadłe.
Udowodnij, że jeżeli liczby niezerowe 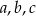 spełniają warunek
spełniają warunek 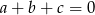 to
to
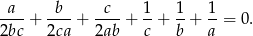
W pewnej szkole 20% uczniów uczęszcza na kółko plastyczne, a 34% uczniów uczęszcza na kółko muzyczne. Wiadomo ponadto, że 58% uczniów nie uczęszcza na żadne z tych kółek. Oblicz jakie jest prawdopodobieństwo, że losowy wybrany uczeń tej szkoły uczęszcza jednocześnie na kółko plastyczne i muzyczne.
Wykaż, że liczba 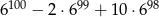 jest podzielna przez 17.
jest podzielna przez 17.
Punkty 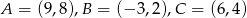 są wierzchołkami trójkąta. Wysokość trójkąta poprowadzona z wierzchołka
są wierzchołkami trójkąta. Wysokość trójkąta poprowadzona z wierzchołka 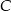 przecina prostą
przecina prostą 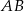 w punkcie
w punkcie 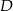 . Oblicz współrzędne punktu
. Oblicz współrzędne punktu 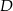 .
.
Oblicz objętość ostrosłupa prawidłowego trójkątnego o krawędzi podstawy długości 6 cm i krawędzi bocznej długości 8 cm.
Droga z miasta 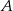 do miasta
do miasta 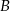 ma długość 474 km. Samochód jadący z miasta
ma długość 474 km. Samochód jadący z miasta 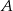 do miasta
do miasta 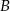 wyrusza godzinę później niż samochód z miasta
wyrusza godzinę później niż samochód z miasta 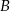 do miasta
do miasta 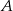 . Samochody te spotykają się w odległości 300 km od miasta
. Samochody te spotykają się w odległości 300 km od miasta 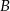 . Średnia prędkość samochodu, który wyjechał z miasta
. Średnia prędkość samochodu, który wyjechał z miasta 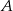 , liczona od chwili wyjazdu z
, liczona od chwili wyjazdu z 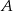 do momentu spotkania, była o 17 km/h mniejsza od średniej prędkości drugiego samochodu liczonej od chwili wyjazdu z
do momentu spotkania, była o 17 km/h mniejsza od średniej prędkości drugiego samochodu liczonej od chwili wyjazdu z 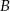 do chwili spotkania. Oblicz średnią prędkość każdego samochodu do chwili spotkania.
do chwili spotkania. Oblicz średnią prędkość każdego samochodu do chwili spotkania.

