/Szkoła średnia/Zadania maturalne/Matura 2015
Egzamin Maturalny
z Matematyki (termin dodatkowy)
poziom podstawowy (technikum) 2 czerwca 2015 Czas pracy: 170 minut
Zadania zamknięte
Liczba 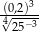 jest równa
jest równa
A) 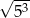 B)
B) 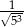 C)
C) 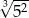 D)
D) 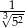
Przy 23-procentowej stawce podatku VAT cena brutto samochodu jest równa 45 018 zł. Jaka jest cena netto tego samochodu?
A) 34 663,86 zł B) 36 600 zł C) 44 995 zł D) 55 372,14 zł
Wskaż nierówność, która opisuje zaznaczony na osi przedział otwarty 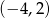 .
.
![]()
A) 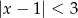 B)
B) 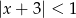 C)
C) 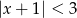 D)
D) 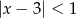
Liczba 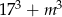 jest podzielna przez 19 dla
jest podzielna przez 19 dla
A) 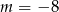 B)
B) 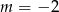 C)
C) 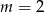 D)
D) 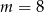
Dla 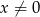 równanie
równanie 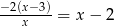
A) nie ma rozwiązań
B) ma dokładnie jedno rozwiązanie
C) ma dwa różne rozwiązania
D) ma trzy różne rozwiązania
Równanie 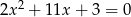
A) nie ma rozwiązań rzeczywistych.
B) ma dokładnie jedno rozwiązanie rzeczywiste.
C) ma dwa dodatnie rozwiązania rzeczywiste.
D) ma dwa ujemne rozwiązania rzeczywiste.
Do dziedziny funkcji 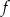 określonej wzorem
określonej wzorem 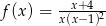 nie mogą należeć liczby
nie mogą należeć liczby
A) 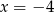 i
i 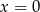 B)
B) 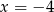 i
i 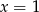 C)
C) 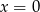 i
i 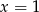 D)
D) 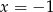 i
i 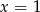
Wyrażenie 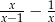 , określone dla
, określone dla 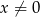 i
i 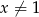 , jest równe
, jest równe
A) 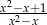 B)
B) 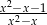 C)
C) 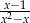 D)
D) 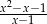
Liczba 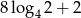 jest równa
jest równa
A) 8 B) 6 C) 4 D) 3,5
Najmniejszą wartością funkcji kwadratowej 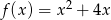 jest
jest
A) 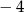 B)
B) 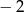 C) 0 D) 4
C) 0 D) 4
Na rysunku przedstawiono fragment wykresu pewnej funkcji liniowej 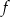 .
.
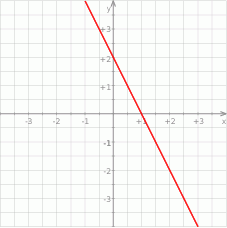
Funkcja liniowa 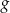 , której wykres jest symetryczny do wykresu funkcji
, której wykres jest symetryczny do wykresu funkcji 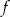 względem poziomej osi układu współrzędnych, jest określona wzorem
względem poziomej osi układu współrzędnych, jest określona wzorem
A) 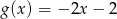 B)
B) 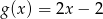 C)
C) 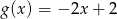 D)
D) 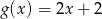
Ciąg arytmetyczny 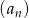 jest określony wzorem
jest określony wzorem 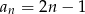 , dla
, dla 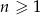 . Suma stu początkowych kolejnych wyrazów tego ciągu jest równa
. Suma stu początkowych kolejnych wyrazów tego ciągu jest równa
A) 9900 B) 9950 C) 10000 D) 10050
Ciąg 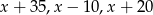 jest geometryczny. Stąd wynika, że
jest geometryczny. Stąd wynika, że
A) 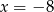 B)
B) 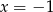 C)
C) 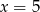 D)
D) 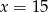
Kąt  jest najmniejszym z kątów trójkąta prostokątnego o bokach długości
jest najmniejszym z kątów trójkąta prostokątnego o bokach długości 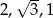 . Wtedy
. Wtedy
A) 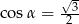 B)
B) 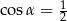 C)
C) 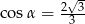 D)
D) 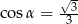
Dla każdego kąta  , spełniającego warunek:
, spełniającego warunek: 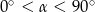 , wyrażenie
, wyrażenie 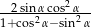 jest równe
jest równe
A) 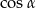 B)
B) 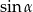 C)
C) 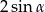 D)
D) 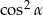
Bok rombu ma taką samą długość jak przekątna kwadratu. Pole rombu jest równe polu kwadratu. Zatem kąt ostry tego rombu ma miarę
A) 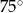 B)
B) 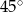 C)
C) 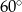 D)
D) 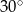
Dane są punkty 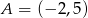 oraz
oraz 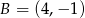 . Promień okręgu opisanego na trójkącie równobocznym
. Promień okręgu opisanego na trójkącie równobocznym 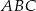 jest równy
jest równy
A) 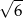 B)
B) 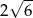 C)
C) 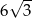 D)
D) 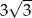
Suma odległości punktu 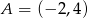 od prostych o równaniach
od prostych o równaniach 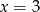 i
i 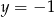 jest równa
jest równa
A) 10 B) 9 C) 8 D) 7
Punkt 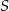 jest środkiem okręgu (patrz rysunek). Zaznaczony kąt
jest środkiem okręgu (patrz rysunek). Zaznaczony kąt  jest równy
jest równy
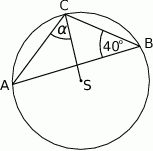
A) 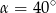 B)
B) 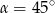 C)
C) 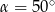 D)
D) 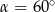
Dany jest stożek, którego przekrojem osiowym jest trójkąt o bokach długości: 6, 10 i 10. Stosunek pola powierzchni bocznej stożka do pola jego podstawy jest równy
A) 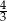 B)
B)  C)
C)  D)
D) 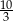
Każda krawędź ostrosłupa prawidłowego trójkątnego ma długość równą 8 . Pole powierzchni całkowitej tego ostrosłupa jest równe
A) 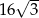 B)
B) 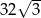 C)
C) 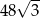 D)
D) 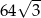
Promień kuli o objętości 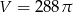 jest równy
jest równy
A) 18 B) 9 C) 8 D) 6
Medianą zestawu danych 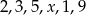 jest liczba 4. Wtedy
jest liczba 4. Wtedy  może być równe
może być równe
A) 2 B) 3 C) 4 D) 5
Ile jest wszystkich liczb naturalnych trzycyfrowych, których iloczyn cyfr jest równy 4?
A) 3 B) 4 C) 6 D) 8
Rzucamy dwa razy symetryczną sześcienną kostką do gry. Prawdopodobieństwo otrzymania iloczynu oczek równego cztery jest równe
A) 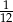 B)
B) 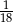 C)
C) 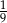 D)
D) 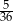
Zadania otwarte
Rozwiąż nierówność 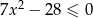 .
.
Rozwiąż równanie 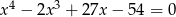 .
.
Funkcja kwadratowa, 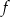 dla
dla 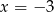 przyjmuje wartość największą równą 4. Do wykresu funkcji
przyjmuje wartość największą równą 4. Do wykresu funkcji 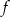 należy punkt
należy punkt 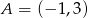 . Zapisz wzór funkcji kwadratowej
. Zapisz wzór funkcji kwadratowej 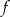 .
.
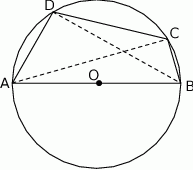
Bok 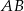 czworokąta
czworokąta 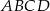 wpisanego w okrąg jest średnicą tego okręgu (zobacz rysunek). Udowodnij, że
wpisanego w okrąg jest średnicą tego okręgu (zobacz rysunek). Udowodnij, że 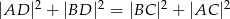 .
.
W siedmiowyrazowym ciągu arytmetycznym środkowy wyraz jest równy 0. Udowodnij, że suma wyrazów tego ciągu jest równa 0.
Ze zbioru cyfr 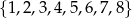 losujemy kolejno dwie cyfry (losowanie bez zwracania) i tworzymy liczby dwucyfrowe tak, że pierwsza wylosowana cyfra jest cyfrą dziesiątek, a druga – cyfrą jedności. Oblicz prawdopodobieństwo utworzenia liczby podzielnej przez 4.
losujemy kolejno dwie cyfry (losowanie bez zwracania) i tworzymy liczby dwucyfrowe tak, że pierwsza wylosowana cyfra jest cyfrą dziesiątek, a druga – cyfrą jedności. Oblicz prawdopodobieństwo utworzenia liczby podzielnej przez 4.
Dany jest romb o boku długości 35. Długości przekątnych tego rombu różnią się o 14. Oblicz pole tego rombu.
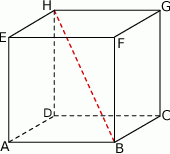
Wysokość prostopadłościanu 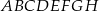 jest równa 1, a długość przekątnej
jest równa 1, a długość przekątnej 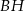 jest równa sumie długości krawędzi
jest równa sumie długości krawędzi 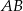 i
i 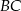 . Oblicz objętość tego prostopadłościanu.
. Oblicz objętość tego prostopadłościanu.
Deweloper oferuje możliwość kompletnego wyposażenia kuchni i salonu w ofercie „Malejące raty”. Wysokość pierwszej raty ustalono na 775 zł. Każda następna rata jest o 10 zł mniejsza od poprzedniej. Całkowity koszt wyposażenia kuchni i salonu ustalono na 30 240 zł. Oblicz wysokość ostatniej raty i liczbę wszystkich rat.

