/Szkoła średnia/Zadania maturalne/Matura 2015
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony
(technikum) 25 kwietnia 2015 Czas pracy: 180 minut
Wyznacz wszystkie wartości parametru 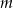 , dla których równanie
, dla których równanie 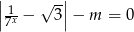 ma dwa pierwiastki, których iloczyn jest ujemny.
ma dwa pierwiastki, których iloczyn jest ujemny.
Długości boków prostokąta 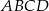 spełniają warunki:
spełniają warunki: 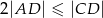 i
i 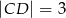 . Na boku
. Na boku 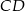 wybrano punkty
wybrano punkty 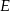 i
i 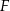 w ten sposób, że
w ten sposób, że 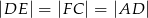 . Punkt
. Punkt 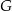 jest takim punktem odcinka
jest takim punktem odcinka 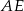 , że
, że 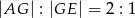 . Oblicz długość boku
. Oblicz długość boku 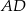 prostokąta, dla której pole trójkąta
prostokąta, dla której pole trójkąta 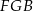 jest największe.
jest największe.
Wielomian 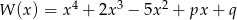 jest podzielny przez dwumian
jest podzielny przez dwumian 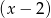 , a przy dzieleniu przez
, a przy dzieleniu przez 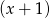 daje resztę
daje resztę 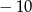 . Wyznacz
. Wyznacz 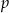 i
i 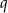 .
.
Rozwiąż nierówność
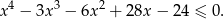
W półkole o promieniu  wpisano trapez równoramienny. Przekątna trapezu o długości
wpisano trapez równoramienny. Przekątna trapezu o długości 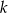 tworzy z dłuższą podstawą kąt o mierze
tworzy z dłuższą podstawą kąt o mierze  , a krótsza podstawa trapezu ma długość
, a krótsza podstawa trapezu ma długość  . Uzasadnij, że
. Uzasadnij, że 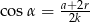 .
.
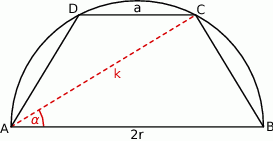
Wyznacz wszystkie wartości parametru 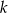 , dla których równanie
, dla których równanie 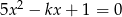 ma dwa różne pierwiastki, których różnica jest liczbą z przedziału
ma dwa różne pierwiastki, których różnica jest liczbą z przedziału 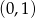 .
.
Uzasadnij, że jeżeli liczby niezerowe 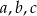 spełniają warunek
spełniają warunek 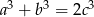 to
to
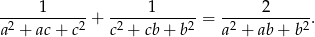
Okrąg wpisany w trójkąt 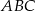 ma równanie
ma równanie 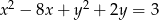 . Oblicz
. Oblicz 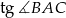 jeżeli
jeżeli 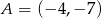 .
.
Ze zbioru liczb 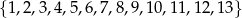 losujemy bez zwracania 4 liczby. Oblicz jakie jest prawdopodobieństwo, że wśród 4 otrzymanych liczb jest dokładnie jedna para liczb o sumie równej 14.
losujemy bez zwracania 4 liczby. Oblicz jakie jest prawdopodobieństwo, że wśród 4 otrzymanych liczb jest dokładnie jedna para liczb o sumie równej 14.
W ostrosłupie prawidłowym trójkątnym krawędź boczna ma długość 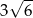 , a krawędź podstawy ma długość 12. Oblicz miarę kąta utworzonego przez dwie sąsiednie ściany boczne.
, a krawędź podstawy ma długość 12. Oblicz miarę kąta utworzonego przez dwie sąsiednie ściany boczne.
Liczbę 255 przedstaw jako sumę czterech całkowitych składników będących kolejnymi wyrazami ciągu geometrycznego tak, aby trzeci wyraz był o 45 większy od wyrazu pierwszego.

