/Szkoła średnia/Zadania maturalne/Matura 2015
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony 28 lutego 2015 Czas pracy: 180 minut
Zadania zamknięte
Wielomian 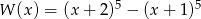 zapisano w postaci
zapisano w postaci 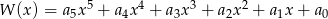 . Suma
. Suma 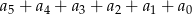 jest równa
jest równa
A) 275 B) 0 C) 1 D) 211
Pierwszy wyraz nieskończonego ciągu geometrycznego jest równy 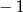 , a suma wszystkich jego wyrazów jest równa ilorazowi tego ciągu. Drugi wyraz tego ciągu jest równy
, a suma wszystkich jego wyrazów jest równa ilorazowi tego ciągu. Drugi wyraz tego ciągu jest równy
A) 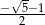 B)
B) 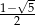 C)
C) 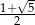 D)
D) 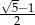
Funkcja określona dla każdej liczby rzeczywistej  wzorem
wzorem 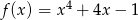
A) ma więcej niż dwa minima lokalne.
B) ma dokładnie dwa minima lokalne.
C) ma dokładnie jedno minimum lokalne.
D) nie ma minimum lokalnego.
Wskaż równanie okręgu opisanego na trójkącie 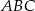 o wierzchołkach
o wierzchołkach 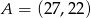 ,
, 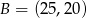 ,
, 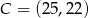
A) 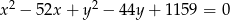
B) 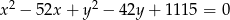
C) 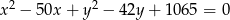
D) 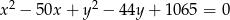
Liczba 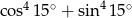 jest równa
jest równa
A) 1 B)  C)
C) 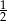 D)
D) 
Zadania otwarte
Rozwiąż równanie 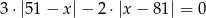 .
.
Oblicz 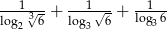 .
.
Wyznacz punkty wspólne wykresów 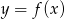 i
i 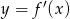 jeżeli
jeżeli 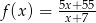 .
.
Prosta 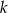 przechodząca przez punkt przecięcia przekątnych trapezu
przechodząca przez punkt przecięcia przekątnych trapezu 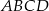 przecina jego podstawy
przecina jego podstawy 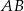 i
i 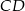 odpowiednio w punktach
odpowiednio w punktach 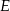 i
i 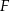 . Wykaż, że
. Wykaż, że 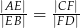 .
.
Oblicz granicę 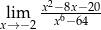 .
.
Wyznacz wszystkie wartości parametru 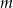 , dla których okrąg o równaniu
, dla których okrąg o równaniu 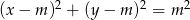 jest styczny do prostej
jest styczny do prostej 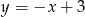 .
.
Sinus kąta jaki tworzą przekątne prostokąta o polu 60 jest równy 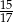 . Oblicz obwód tego prostokąta.
. Oblicz obwód tego prostokąta.
Oblicz miarę kąta ostrego pod jakim przecinają się styczne do wykresu funkcji
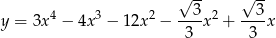
poprowadzone w punktach o pierwszych współrzędnych równych 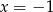 i
i 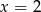 .
.
Rozwiąż równanie 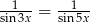 w przedziale
w przedziale 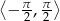 .
.
Ciąg 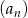 , gdzie
, gdzie 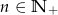 , określony jest następująco:
, określony jest następująco:
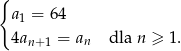
Wyznacz wszystkie wartości 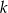 , dla których suma
, dla których suma 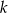 początkowych wyrazów ciągu
początkowych wyrazów ciągu 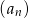 jest równa
jest równa 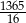 .
.
Wykaż, że jeżeli 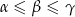 są kątami wewnętrznymi trójkąta rozwartokątnego, to
są kątami wewnętrznymi trójkąta rozwartokątnego, to
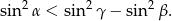
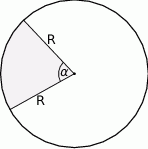
Z papierowego koła o promieniu 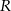 wycięto wycinek kołowy, który jest powierzchnią boczną stożka o maksymalnej objętości. Jaka była miara kąta środkowego
wycięto wycinek kołowy, który jest powierzchnią boczną stożka o maksymalnej objętości. Jaka była miara kąta środkowego  wyciętego wycinka? Wynik podaj w radianach.
wyciętego wycinka? Wynik podaj w radianach.
Do windy na parterze budynku wsiadło 8 osób, po czym każda z nich w sposób losowy wysiadła na jednym z pięciu pięter budynku. Jakie jest prawdopodobieństwo, że na jednym z pięter wysiadło co najmniej 6 osób?

