/Szkoła średnia/Zadania maturalne/Matura 2015
Lubelska próba przed maturą
z matematyki (dla klas drugich)
poziom podstawowy grupa II 3 czerwca 2015 Czas pracy: 170 minut
Zadania zamknięte
Liczba 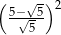 jest równa
jest równa
A) 4 B) 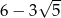 C)
C) 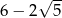 D) 6
D) 6
Liczba 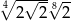 jest równa
jest równa
A) 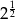 B) 2 C)
B) 2 C) 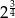 D)
D) 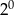
Wiedząc, że 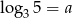 , określ wartość wyrażenia
, określ wartość wyrażenia 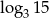 jest równa
jest równa
A) 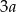 B)
B) 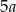 C)
C) 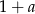 D)
D) 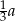
Podwojony kwadrat różnicy dwóch liczb  i
i 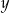 można zapisać w postaci
można zapisać w postaci
A) 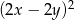 B)
B) 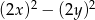 C)
C) 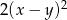 D)
D) 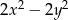
W trójkącie równobocznym długość każdego boku zmniejszono o 20%. Wtedy pole tego trójkąta
A) zmniejszy się o 36%
B) zmniejszy się o 20%
C) zmniejszy się o 40%
D) zmniejszy się o mniej niż 20%
Punkty 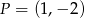 i
i 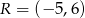 są dwoma sąsiednimi wierzchołkami kwadratu
są dwoma sąsiednimi wierzchołkami kwadratu 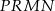 . Przekątna tego kwadratu ma długość
. Przekątna tego kwadratu ma długość
A) 10 B) 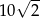 C)
C) 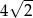 D) 8
D) 8
Wyrażenie 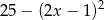 jest równe
jest równe
A) 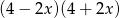 B)
B) 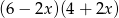 C)
C) 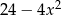 D)
D) 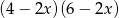
Dane są dwa okręgi styczne zewnętrznie o promieniach 6 i 13. Odległość między środkami tych okręgów jest równa
A) 7 B) 13 C) 10 D) 19
Miejscem zerowym funkcji liniowej 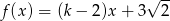 jest liczba
jest liczba 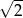 jeśli
jeśli
A) 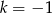 B)
B) 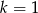 C)
C) 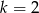 D)
D) 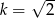
Wierzchołek paraboli ma współrzędne 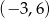 . Punkt
. Punkt 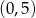 należy do paraboli. Zbiorem wartości funkcji jest
należy do paraboli. Zbiorem wartości funkcji jest
A) 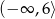 B)
B) 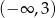 C)
C) 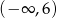 D)
D) 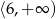
Liczby 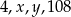 tworzą ciąg geometryczny, wtedy
tworzą ciąg geometryczny, wtedy
A) 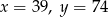 B)
B) 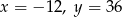 C)
C) 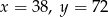 D)
D) 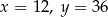
Ciąg 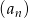 jest określony wzorem
jest określony wzorem 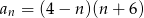 dla
dla 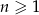 . Liczba dodatnich wyrazów tego ciągu jest równa
. Liczba dodatnich wyrazów tego ciągu jest równa
A) 10 B) 8 C) 3 D) 4
Wykresem funkcji kwadratowej 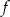 jest parabola o wierzchołku
jest parabola o wierzchołku 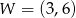 . Wówczas prawdziwa jest równość
. Wówczas prawdziwa jest równość
A) 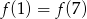 B)
B) 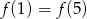 C)
C) 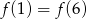 D)
D) 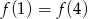
Funkcja
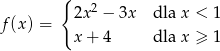
dla argumentu 2 przyjmuje wartość:
A) 6 B) 2 C) 0 D) 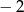
Iloczyn pierwiastków równania 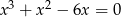 jest równy
jest równy
A) 1 B) 3 C) 0 D) 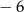
Punkt 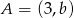 należy do wykresu funkcji
należy do wykresu funkcji 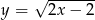 , gdzie
, gdzie 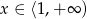 . Wtedy
. Wtedy
A) 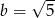 B)
B) 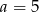 C)
C) 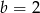 D)
D) 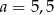
Kąt środkowy i kąt wpisany w okrąg są oparte na tym samym łuku. Suma ich miar jest równa 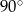 . Miara kata środkowego jest równa
. Miara kata środkowego jest równa
A) 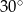 B)
B) 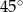 C)
C) 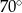 D)
D) 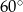
Zbiorem rozwiązań nierówności 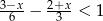 jest przedział
jest przedział
A) 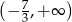 B)
B) 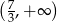 C)
C) 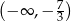 D)
D) 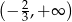
Liczba 3 jest przybliżeniem z niedomiarem liczby 3,2. Błąd względny tego przybliżenia jest równy
A) 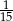 B) 2 C)
B) 2 C) 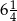 D)
D) 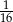
Dla pewnego argumentu funkcje 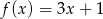 i
i 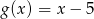 przyjmują taką samą wartość. Jaka to wartość?
przyjmują taką samą wartość. Jaka to wartość?
A) 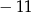 B)
B) 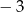 C)
C) 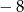 D) 3
D) 3
Ile wynosi 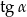 jeśli
jeśli 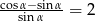 ?
?
A) 3 B) 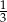 C)
C) 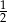 D) 2
D) 2
Rozwiązanie 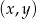 układu równań
układu równań 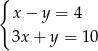 spełnia warunki
spełnia warunki
A) 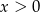 i
i 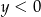 B)
B) 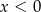 i
i 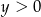 C)
C) 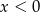 i
i 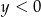 D)
D) 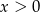 i
i 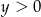
Miary kątów trójkąta pozostają w stosunku 4:5:6. Miary kątów tego trójkąta są równe
A) 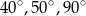 B)
B) 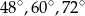 C)
C) 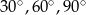 D)
D) 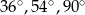
Dla jakiej wartości parametru 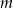 punkt przecięcia prostych
punkt przecięcia prostych 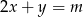 i
i 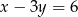 należy do osi
należy do osi 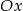 ?
?
A) dla 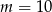 B) dla
B) dla 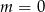 C) dla
C) dla 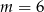 D) dla
D) dla 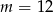
Pole powierzchni jednej ściany sześcianu jest równe 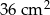 . Objętość tego sześcianu jest równa
. Objętość tego sześcianu jest równa
A) 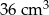 B)
B) 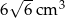 C)
C) 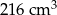 D)
D) 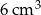
Aby otrzymać wykres funkcji 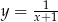 należy wykres funkcji
należy wykres funkcji 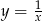 przesunąć o 1 jednostkę
przesunąć o 1 jednostkę
A) w dół B) w lewo C) w górę D) w prawo
Zadania otwarte
Różnica kwadratów dwóch kolejnych liczb naturalnych wynosi 17. Wyznacz te liczby.
Wykaż, że liczba 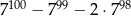 jest podzielna przez 4.
jest podzielna przez 4.
Rozwiąż równanie 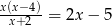 , dla
, dla 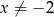 .
.
Sprawdź, czy trójkąt o bokach: 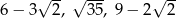 jest trójkątem prostokątnym.
jest trójkątem prostokątnym.
Ile kwadratowych płytek o boku 3 dm potrzeba do wyłożenia dna i wewnętrznych ścian basenu o długości 9 m, szerokości 6 m i głębokości 3 m ?
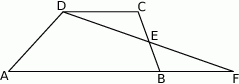
Na rysunku przedstawiono trapez 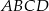 i trójkąt
i trójkąt 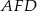 . Punkt
. Punkt 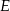 leży w połowie odcinka
leży w połowie odcinka 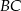 . Uzasadnij, że pole trapezu
. Uzasadnij, że pole trapezu 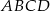 i pole trójkąta
i pole trójkąta 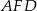 są równe.
są równe.
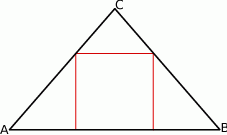
W trójkąt równoramienny 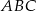 (
(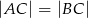 ) o długości podstawy
) o długości podstawy 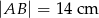 wpisano kwadrat o boku długości 6 cm. Oblicz pole trójkąta
wpisano kwadrat o boku długości 6 cm. Oblicz pole trójkąta 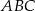 .
.
Liczby 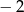 i 3 są pierwiastkami wielomianu
i 3 są pierwiastkami wielomianu 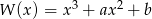 . Wyznacz liczby
. Wyznacz liczby  i
i 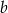 oraz trzeci pierwiastek wielomianu.
oraz trzeci pierwiastek wielomianu.
Dwie krawcowe mają uszyć pewną ilość kurtek. Jeżeli będą pracowały razem to wykonają pracę w ciągu 20 dni. Pierwsza z nich wykonałaby zlecenie samodzielnie w ciągu 36 dni. Ile dni potrzebowałaby druga krawcowa na samodzielne wykonanie tej pracy?

