/Szkoła średnia/Zadania maturalne/Matura 2015
Próbny Egzamin Maturalny
z Matematyki poziom rozszerzony 18 grudnia 2014 Czas pracy: 180 minut
Zadania zamknięte
Wielomian 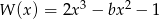 jest podzielny przez dwumian
jest podzielny przez dwumian 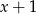 . Wynika stąd, że
. Wynika stąd, że
A) 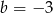 B)
B) 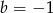 C)
C) 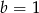 D)
D) 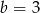
Okrąg o równaniu 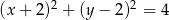 ma dwa punkty wspólne z prostą o równaniu
ma dwa punkty wspólne z prostą o równaniu
A) 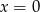 B)
B) 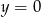 C)
C) 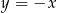 D)
D) 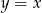
Funkcja określona dla każdej liczby rzeczywistej  wzorem
wzorem 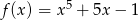
A) ma więcej niż dwa minima lokalne.
B) ma dokładnie dwa minima lokalne.
C) ma dokładnie jedno minimum lokalne.
D) nie ma minimum lokalnego.
Każda liczba  należąca do przedziału otwartego
należąca do przedziału otwartego 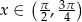 spełnia nierówność
spełnia nierówność
A) 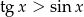 B)
B) 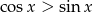 C)
C) 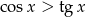 D)
D) 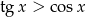
Funkcja 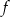 jest określona dla wszystkich liczb rzeczywistych wzorem
jest określona dla wszystkich liczb rzeczywistych wzorem 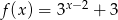 . Prosta
. Prosta 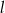 ma równanie
ma równanie 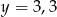 . Ile punktów wspólnych mają wykres funkcji
. Ile punktów wspólnych mają wykres funkcji 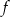 i prosta
i prosta 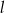 ?
?
A) Zero. B) Jeden. C) Dwa. D) Nieskończenie wiele.
Zadania otwarte
Dane są liczby 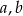 takie, że
takie, że 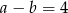 i
i 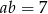 . Oblicz
. Oblicz 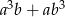 .
.
Długości boków prostokąta są równe 3 oraz 5. Oblicz sinus kąta ostrego, który tworzą przekątne tego prostokąta.
Oblicz granicę 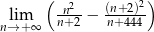 .
.
Funkcja 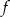 jest określona wzorem
jest określona wzorem 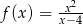 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej 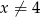 . Oblicz pochodną funkcji
. Oblicz pochodną funkcji 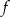 w punkcie
w punkcie 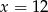 .
.
Funkcja 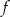 jest określona wzorem
jest określona wzorem 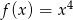 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  . Wyznacz równanie prostej stycznej do wykresu funkcji
. Wyznacz równanie prostej stycznej do wykresu funkcji 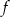 , która jest równoległa do prostej
, która jest równoległa do prostej 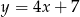 .
.
Wyznacz wszystkie liczby rzeczywiste  , spełniające równanie
, spełniające równanie 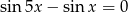 .
.
Niech 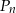 oznacza pole koła o promieniu
oznacza pole koła o promieniu 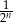 , dla
, dla 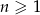 . Oblicz sumę wszystkich wyrazów ciągu
. Oblicz sumę wszystkich wyrazów ciągu 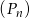 .
.
Wykaż, że jeżeli 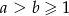 , to
, to 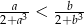 .
.
Wykaż, że jeżeli 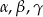 są kątami wewnętrznymi trójkąta i
są kątami wewnętrznymi trójkąta i 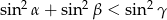 , to
, to 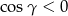 .
.
Punkt 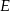 jest środkiem boku
jest środkiem boku 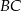 prostokąta
prostokąta 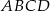 , w którym
, w którym 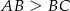 . Punkt
. Punkt 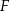 leży na boku
leży na boku 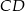 tego prostokąta oraz
tego prostokąta oraz 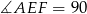 . Udowodnij, że
. Udowodnij, że 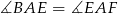 .
.
Oblicz prawdopodobieństwo warunkowe, że w trzykrotnym rzucie symetryczną sześcienną kostką do gry otrzymamy co najmniej jedną „jedynkę”, pod warunkiem że otrzymamy co najmniej jedną „szóstkę”.
Dany jest okrąg 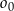 o równaniu
o równaniu 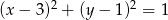 . W pierwszej „ćwiartce” układu współrzędnych istnieją dwa okręgi
. W pierwszej „ćwiartce” układu współrzędnych istnieją dwa okręgi 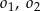 styczne zewnętrznie do okręgu
styczne zewnętrznie do okręgu 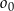 i jednocześnie styczne do obu osi układu współrzędnych. Oblicz odległość środków okręgów
i jednocześnie styczne do obu osi układu współrzędnych. Oblicz odległość środków okręgów 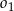 oraz
oraz 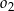 .
.
Okno na poddaszu ma mieć kształt trapezu równoramiennego, którego krótsza podstawa i ramiona mają długość po 4 dm. Oblicz, jaką długość powinna mieć dłuższa podstawa tego trapezu, aby do pomieszczenia wpadało przez to okno jak najwięcej światła, czyli aby pole powierzchni okna było największe. Oblicz to pole.

