/Szkoła średnia/Zadania maturalne/Matura 2015
Lubelska próba przed maturą
z matematyki poziom podstawowy grupa I 25 lutego 2015 Czas pracy: 170 minut
Zadania zamknięte
Liczba 25 jest przybliżeniem z niedomiarem liczby  . Błąd bezwzględny tego przybliżenia jest równy 0,39. Liczba
. Błąd bezwzględny tego przybliżenia jest równy 0,39. Liczba  to
to
A) 25,39 B) 24,61 C) 25,61 D) 24,39
Liczba 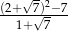 jest równa
jest równa
A) 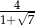 B) 4 C)
B) 4 C) 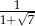 D) 2
D) 2
Wiadomo, że prosta o równaniu 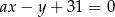 przechodzi przez środek odcinka o końcach
przechodzi przez środek odcinka o końcach 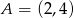 i
i 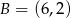 . Wówczas wartość współczynnika
. Wówczas wartość współczynnika  jest równa
jest równa
A) 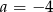 B)
B) 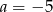 C)
C) 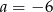 D)
D) 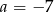
Cenę komputera obniżano dwukrotnie, najpierw o 20%, a po miesiącu jeszcze o 10%. W wyniku obu obniżek cena komputera zmniejszyła się o
A) 31% B) 30% C) 29% D) 28%
Wartość liczbowa wyrażenia 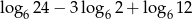 jest równa
jest równa
A) 2 B) 3 C) 4 D) 5
Prostą prostopadłą do prostej o równaniu 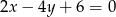 jest prosta o równaniu
jest prosta o równaniu
A) 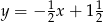 B)
B) 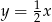 C)
C) 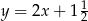 D)
D) 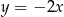
Wartość wyrażenia 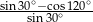 jest równa
jest równa
A) 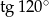 B) 2 C) 1 D)
B) 2 C) 1 D) 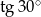
Jeżeli punkty 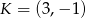 i
i 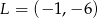 są środkami nierównoległych boków prostokąta, to długość przekątnej tego prostokąta jest równa
są środkami nierównoległych boków prostokąta, to długość przekątnej tego prostokąta jest równa
A) 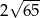 B)
B) 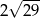 C)
C) 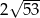 D)
D) 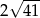
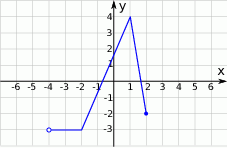
Na rysunku przedstawiony jest wykres funkcji  . Dziedziną funkcji
. Dziedziną funkcji  jest
jest
A) 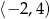 B)
B) 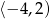 C)
C) 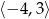 D)
D) 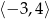
Liczba  należy do dziedziny funkcji
należy do dziedziny funkcji 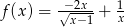 jeżeli
jeżeli
A) 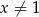 B)
B) 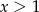 C)
C) 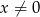 D)
D) 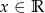
Ile wynosi pole trójkąta, w którym dwa boki mają długości 7 i 12, a kąt zawarty między nimi wynosi 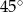 ?
?
A) 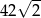 B) 42 C)
B) 42 C) 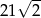 D) 21
D) 21
Największa wartość funkcji 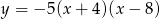 wynosi
wynosi
A) 140 B) 150 C) 160 D) 180
Jeżeli różnica miedzy dwiema liczbami jest równa 5, a różnica między ich kwadratami wynosi 85, to suma tych liczb jest równa
A) 15 B) 16 C) 17 D) 18
Pole trójkąta prostokątnego jest równe 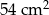 . Różnica długości przyprostokątnych wynosi 3 cm. Jaką długość ma przeciwprostokątna tego trójkąta?
. Różnica długości przyprostokątnych wynosi 3 cm. Jaką długość ma przeciwprostokątna tego trójkąta?
A) 14 B) 15 C) 16 D) 17
Dana jest funkcja 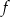 określona wzorem
określona wzorem 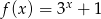 . Wartość funkcji
. Wartość funkcji 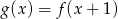 dla argumentu
dla argumentu 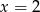 jest równa
jest równa
A) 28 B) 16 C) 25 D) 10
Najmniejszą liczbą całkowitą należącą do zbioru rozwiązań nierówności 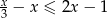 jest
jest
A) 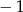 B) 0 C) 1 D) 2
B) 0 C) 1 D) 2
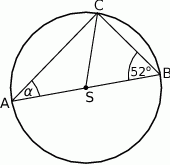
Miara kąta  trójkąta
trójkąta  wpisanego w okrąg o środku
wpisanego w okrąg o środku  jest równa
jest równa
A) 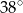 B)
B) 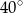 C)
C) 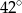 D)
D) 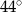
Pierwszy wyraz ciągu arytmetycznego jest równy 5, a suma jego pięciu początkowych wyrazów wynosi 55. Czwarty wyraz tego ciągu jest równy
A) 12 B) 13 C) 14 D) 15
W tabeli podano dane dotyczące wyników z pracy klasowej z matematyki uzyskanych w pewnej klasie.
| Liczba uczniów | 3 | 6 | 8 | 4 | 4 | 2 |
| Ocena | 1 | 2 | 3 | 4 | 5 | 6 |
Różnica średniej arytmetycznej ocen i mediany wynosi
A) 0,2 B)  C)
C) 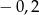 D)
D) 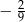
Dany jest ciąg liczbowy 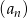 , w którym
, w którym 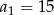 ,
, 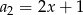 ,
, 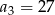 . Dla jakiej wartości liczbowej
. Dla jakiej wartości liczbowej  dany ciąg jest ciągiem arytmetycznym?
dany ciąg jest ciągiem arytmetycznym?
A) 8 B) 9 C) 10 D) 11
Ze zbioru liczb naturalnych dwucyfrowych nie mniejszych od 50 losujemy jedną liczbę. Jakie jest prawdopodobieństwo, że wylosowana liczba będzie podzielna przez 5?
A) 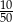 B)
B) 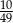 C)
C) 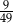 D)
D) 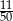
Wykres funkcji kwadratowej 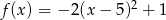 ma dwa punkty wspólne z prostą
ma dwa punkty wspólne z prostą
A) 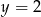 B)
B) 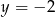 C)
C) 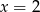 D)
D) 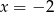
Na rysunku proste 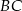 i
i 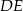 są równoległe oraz
są równoległe oraz 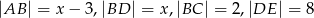 . Wobec tego
. Wobec tego  jest równe
jest równe
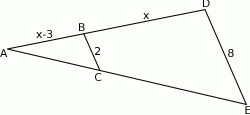
A) 3 B) 3,5 C) 4 D) 4,5
Wysokość trapezu równoramiennego o kącie ostrym 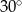 i ramieniu długości
i ramieniu długości 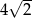 jest równa
jest równa
A) 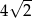 B) 2 C)
B) 2 C) 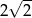 D)
D) 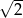
Zadania otwarte
Oblicz najmniejszą wartość funkcji kwadratowej 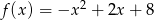 w przedziale
w przedziale 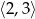 .
.
Rozwiąż nierówność kwadratową 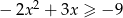 .
.
Wykaż, że liczba 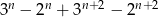 jest podzielna przez 10,
jest podzielna przez 10, 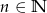 .
.
Na przekątnej 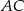 równoległoboku
równoległoboku 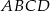 zaznaczono dowolny punkt
zaznaczono dowolny punkt 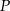 . Udowodnij, że pola trójkątów
. Udowodnij, że pola trójkątów 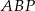 i
i 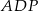 są równe.
są równe.
Dany jest ciąg 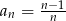 . Wyznacz wzór ogólny ciągu
. Wyznacz wzór ogólny ciągu 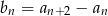 , gdzie
, gdzie 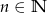 .
.
Prostokątne zdjęcie o szerokości 30 cm i długości 45 cm oprawiono w prostokątną ramkę o jednakowej szerokości. Jaka jest szerokość ramki, jeśli pole zdjęcia wraz z ramką wynosi 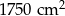 ?
?
Objętość ostrosłupa prawidłowego trójkątnego 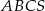 (patrz rysunek) jest równa 36, a promień okręgu opisanego na podstawie
(patrz rysunek) jest równa 36, a promień okręgu opisanego na podstawie 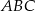 tego ostrosłupa jest równy 4. Oblicz tangens kąta jaki tworzy krawędź boczna z wysokością ostrosłupa.
tego ostrosłupa jest równy 4. Oblicz tangens kąta jaki tworzy krawędź boczna z wysokością ostrosłupa.
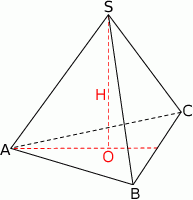
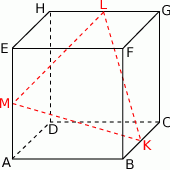
Na krawędziach sześcianu 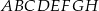 zaznaczono punkty
zaznaczono punkty 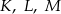 tak, że każdy z nich jest środkiem odpowiedniej krawędzi (patrz rysunek). Oblicz pole trójkąta
tak, że każdy z nich jest środkiem odpowiedniej krawędzi (patrz rysunek). Oblicz pole trójkąta 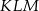 , jeśli krawędź sześcianu ma długość równą 2.
, jeśli krawędź sześcianu ma długość równą 2.
W pojemniku znajdują się dwie kule białe i trzy czerwone. Losujemy dwa razy po jednej kuli bez zwracania. Oblicz prawdopodobieństwo, że wylosujemy co najmniej jedną kulę czerwoną. Wynik przedstaw w postaci ułamka nieskracalnego.

