/Szkoła średnia/Zadania maturalne/Matura 2015
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom rozszerzony
(technikum) 7 marca 2015 Czas pracy: 180 minut
- Narysuj wykresy funkcji
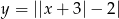 oraz
oraz 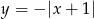 , gdzie
, gdzie 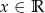 .
. - Wyznacz te wartości parametru
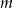 , dla których równanie
, dla których równanie 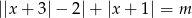 ma dokładnie dwa rozwiązania.
ma dokładnie dwa rozwiązania.
Przez środek okręgu wpisanego w trójkąt równoboczny 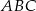 poprowadzono prostą równoległą do boku
poprowadzono prostą równoległą do boku 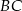 i przecinającą bok
i przecinającą bok 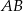 w punkcie
w punkcie 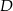 . Oblicz iloraz
. Oblicz iloraz 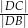 .
.
Dla jakich wartości parametru 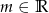 wierzchołek paraboli
wierzchołek paraboli 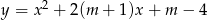 leży najbliżej prostej
leży najbliżej prostej 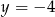 ?
?
Wykaż, że jeżeli liczby rzeczywiste 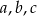 spełniają równość
spełniają równość 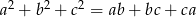 to
to 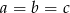 .
.
Wykaż, że jeżeli 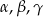 są kątami ostrymi i
są kątami ostrymi i 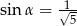 ,
, 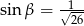 ,
, 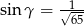 to
to 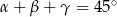 .
.
Przyprostokątna 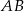 trójkąta prostokątnego
trójkąta prostokątnego 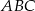 jest zawarta w prostej o równaniu
jest zawarta w prostej o równaniu 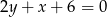 , a środek jego przeciwprostokątnej
, a środek jego przeciwprostokątnej 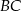 ma współrzędne
ma współrzędne 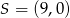 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 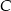 jeżeli
jeżeli 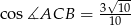 .
.
W skończonym ciągu geometrycznym 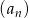 wyraz pierwszy jest równy 2, a wyraz ostatni 39 366. Wiedząc, że suma wszystkich wyrazów wynosi 59 048, oblicz iloraz tego ciągu.
wyraz pierwszy jest równy 2, a wyraz ostatni 39 366. Wiedząc, że suma wszystkich wyrazów wynosi 59 048, oblicz iloraz tego ciągu.
Proste 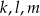 są parami różne i równoległe. Na prostych tych wybrano zbiór
są parami różne i równoległe. Na prostych tych wybrano zbiór 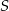 składający się z
składający się z 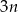 punktów (
punktów (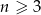 ), przy czym na każdej z prostych wybrano
), przy czym na każdej z prostych wybrano  punktów. Wiadomo ponadto, że jeżeli trzy punkty zbioru
punktów. Wiadomo ponadto, że jeżeli trzy punkty zbioru 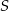 leżą na jednej prostej, to prostą tą jest
leżą na jednej prostej, to prostą tą jest 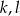 lub
lub 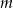 . Oblicz ile jest trójkątów o wierzchołkach należących do zbioru
. Oblicz ile jest trójkątów o wierzchołkach należących do zbioru 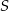 .
.
Suma długości krawędzi graniastosłupa prawidłowego czworokątnego jest równa 16. Dla jakiej długości krawędzi podstawy pole powierzchni całkowitej tego graniastosłupa będzie największe?
Podstawą ostrosłupa 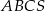 jest trójkąt
jest trójkąt 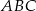 , w którym
, w którym 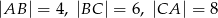 . Wszystkie ściany boczne tworzą z płaszczyzną podstawy kąt
. Wszystkie ściany boczne tworzą z płaszczyzną podstawy kąt 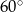 . Oblicz objętość ostrosłupa.
. Oblicz objętość ostrosłupa.
Dany jest czworokąt wypukły 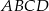 niebędący równoległobokiem. Punkty
niebędący równoległobokiem. Punkty 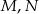 są odpowiednio środkami boków
są odpowiednio środkami boków 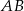 i
i 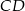 . Punkty
. Punkty 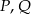 są odpowiednio środkami przekątnych
są odpowiednio środkami przekątnych 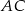 i
i 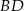 . Uzasadnij, że
. Uzasadnij, że 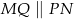 .
.

