/Gimnazjum/Egzamin gimnazjalny/Egzamin 2015
Próbny Egzamin Gimnazjalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info 11 kwietnia 2015 Czas pracy: 90 minut
Informacja do zadań 1 i 2
Koszt ubezpieczenia samochodu w pewnej firmie ubezpieczeniowej jest związany z wiekiem samochodu i polega na tym, że od ceny bazowej ubezpieczenia klient otrzymuje tyle procent zniżki, ile samochód ma lat.
Cena bazowa ubezpieczenia samochodu pana Jacka wynosi 620 zł. Ile zapłaci za to ubezpieczenie pan Jacek, jeżeli jego samochód ma 15 lat? Wybierz odpowiedź spośród podanych.
A) 93 zł B) 527 zł C) 605 zł D) 610 zł
Cena bazowa ubezpieczenia samochodu Pani Uli wynosi 650 zł, ale Pani Ula za ubezpieczenie zapłaciła 598 zł. Ile lat ma samochód Pani Uli? Wybierz odpowiedź spośród podanych.
A) 52 B) 12 C) 8 D) 9
Która równość jest fałszywa? Wybierz odpowiedź spośród podanych.
A) 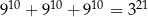 B)
B) 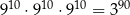
C) 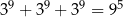 D)
D) 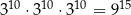
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Liczbą większą od 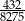 jest
jest
A) 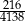 B)
B) 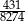 C)
C) 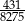 D)
D) 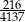
Cena brutto = cena netto + podatek VAT
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Jeżeli cena netto 1 kg gruszek wzrośnie o 100%, to cena bruttoteż wzrośnie o 100%. | P | F |
| Jeżeli cena netto książki wzrośnie o 20 zł, to cena książki z 5% podatkiem VAT wzrośnie o 21 zł. | P | F |
Klasa IIIf wybrała się na wycieczkę składającą się z trzech części. W pierwszej części uczniowie zostali zawiezieni autokarem na miejsce, w którym rozpoczęła się ich piesza wędrówka. W drugiej części odbyli spacer górskim szlakiem, a w ostatniej części zwiedzali leśną ścieżkę dydaktyczną. Na rysunku przedstawiono schemat przebiegu wycieczki.

Na podstawie podanych informacji wybierz zdanie prawdziwe.
A) Cała trasa miała długość 54 km.
B) Uczniowie pokonali autobusem 30 km.
C) Leśna ścieżka dydaktyczna była o 5 km dłuższa od górskiego szlaku.
D) Długość górskiego szlaku była 3 razy mniejsza niż długość leśnej ścieżki dydaktycznej.
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Liczba 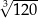 znajduje się na osi liczbowej między
znajduje się na osi liczbowej między
A) 10 i 11 B) 5 i 6 C) 4 i 5 D) 6 i 7
Informacja do zadań 8 i 9
Wykres przedstawia zależność ilości betonu pozostałego w betoniarce (w litrach) od powierzchni wylewki (w 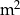 ) wykonanej z tego betonu.
) wykonanej z tego betonu.

Ile betonu zużyto na wykonanie 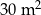 wylewki? Wybierz odpowiedź spośród podanych.
wylewki? Wybierz odpowiedź spośród podanych.
A) 1000 litrów B) 1500 litrów C) 2000 litrów D) 1800 litrów
Ile betonu potrzeba na wykonanie 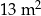 wylewki? Wybierz odpowiedź spośród podanych.
wylewki? Wybierz odpowiedź spośród podanych.
A) 1850 litrów B) 600 litrów C) 650 litrów D) 700 litrów
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Liczba 81390 jest liczbą podzielną przez 60. | P | F |
| Liczba 46125 jest wielokrotnością 375. | P | F |
Prędkość średnia piechura na trasie 20 km wyniosła 5 km/h, a prędkość średnia rowerzysty na tej samej trasie była równa 10 km/h. O ile minut więcej zajęło pokonanie tej trasy piechurowi niż rowerzyście? Wybierz odpowiedź spośród podanych.
A) 180 minut B) 120 minut C) 90 minut D) 60 minut
Do prostopadłościennego akwarium, o wymiarach podanych na rysunku, wlano 200 litrów wody.
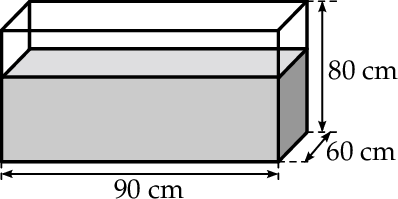
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Wysokość na jaką sięga woda w akwarium jest równa 40 cm. | P | F |
| Gdyby do akwarium dolać 50 litrów wody, to poziom wody podniósłby się o 10 cm. | P | F |
W prostokątnym układzie współrzędnych przedstawiono wykres funkcji, która jest określona dla liczb z przedziału 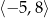 .
.
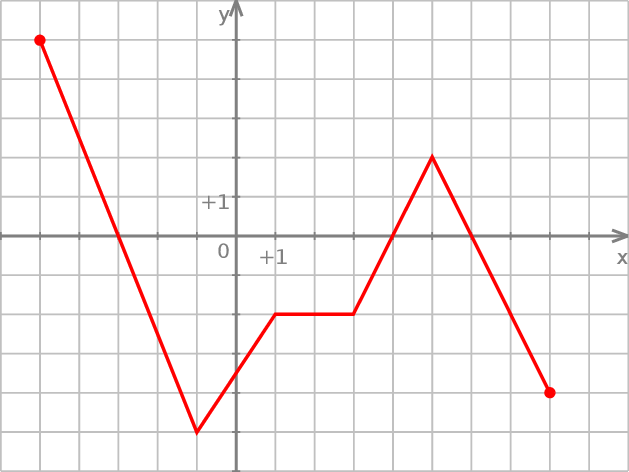
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Funkcja przyjmuje wartość 1 dla argumentów 4 i 6. | P | F |
Funkcja przyjmuje wartość 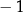 dla trzech różnych argumentów. dla trzech różnych argumentów. | P | F |
Funkcja przyjmuje wartość 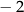 dla więcej niż 3 różnych argumentów. dla więcej niż 3 różnych argumentów. | P | F |
Dla argumentów z przedziału 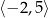 wartości funkcji są ujemne. wartości funkcji są ujemne. | P | F |
Organizatorzy konkursu z języka polskiego przygotowali zestaw, w którym było 15 pytań z gramatyki i 7 pytań z ortografii. Uczestnicy konkursu losowali kolejno po jednym pytaniu, które po wylosowaniu było usuwane z zestawu. Pierwszy uczestnik wylosował pytanie z gramatyki.
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Prawdopodobieństwo wyciągnięcia przez drugą osobę pytania z ortografii zwiększyło się. | P | F |
Prawdopodobieństwo wyciągnięcia przez drugą osobę pytania z gramatyki jest równe  . . | P | F |
Wojtek codziennie, przez tydzień, odczytywał o 8 rano temperaturę powietrza. Oto podane (w 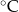 ) wyniki jego pomiarów:
) wyniki jego pomiarów: 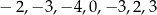 .
.

Wybierz odpowiedź, w której podano poprawne wartości średniej arytmetycznej, mediany i amplitudy (różnica między wartością najwyższą i wartością najniższą) zanotowanych temperatur.
Punkt 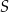 jest środkiem okręgu wpisanego w trójkąt
jest środkiem okręgu wpisanego w trójkąt 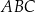 , a punkty
, a punkty 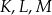 są punktami styczności tego okręgu z bokami trójkąta. Odcinek
są punktami styczności tego okręgu z bokami trójkąta. Odcinek 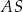 ma długość 26 cm, a odcinek
ma długość 26 cm, a odcinek 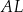 ma długość 24 cm.
ma długość 24 cm.
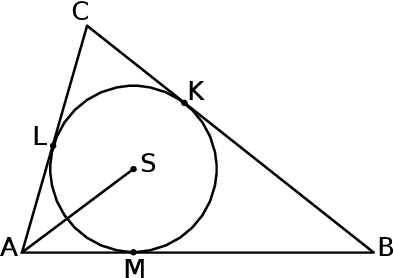
Oceń prawdziwość podanych zdań. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
Promień okręgu wpisanego w trójkąt 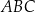 jest równy 9 cm. jest równy 9 cm. | P | F |
Odcinki 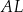 i i 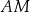 mają tę samą długość. mają tę samą długość. | P | F |
Oskar wykonał model prostopadłościanu. Układał i sklejał ze sobą kolejno drewniane klocki sześcienne o krawędzi 4 cm wzdłuż każdej ściany prostopadłościennego pudełka o wymiarach: 36 cm, 28 cm, 20 cm. Na rysunku przedstawiono część wykonanego modelu (model jest w środku pusty).
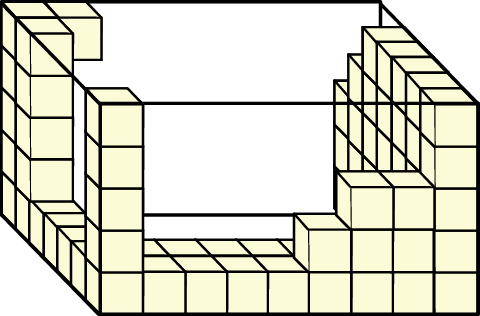
Ile klocków łącznie zużył Oskar na wykonanie całego modelu? Wybierz odpowiedź spośród podanych.
A) 315 B) 230 C) 246 D) 210
Kąt ostry rombu ma miarę 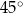 , a jego bok ma długość
, a jego bok ma długość  .
.
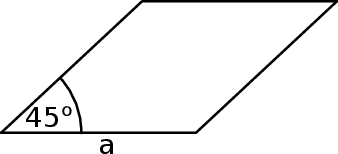
Dokończ zdanie tak, aby otrzymać zdanie prawdziwe.
Pole tego rombu można wyrazić wzorem
A) 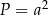 B)
B) 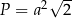 C)
C) 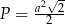 D)
D) 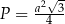
Maciek rysuje siatkę ostrosłupa prawidłowego, którego podstawą jest kwadrat o środku w punkcie 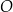 i boku długości 6.
i boku długości 6.
Czy trójkąt 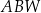 o bokach długości odpowiednio: 6, 5, 5 może być ścianą boczną takiego ostrosłupa? Wybierz odpowiedź T lub N i jej uzasadnienie spośród zdań A–C.
o bokach długości odpowiednio: 6, 5, 5 może być ścianą boczną takiego ostrosłupa? Wybierz odpowiedź T lub N i jej uzasadnienie spośród zdań A–C.
| Tak | Nie |
| ponieważ | |
| A) | trójkąt 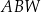 jest równoramienny. jest równoramienny. |
| B) | odległość 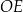 jest mniejsza niż wysokość jest mniejsza niż wysokość 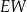 trójkąta trójkąta 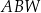 . . |
| C) | odległość 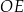 jest większa niż wysokość jest większa niż wysokość 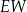 trójkąta trójkąta 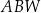 . . |
Zbiornik na wodę ma kształt walca, którego podstawa (dno zbiornika) ma średnicę 10 m. Do zbiornika wlano 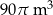 wody, która wypełniła go do
wody, która wypełniła go do 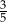 głębokości.
głębokości.
Jaka jest głębokość tego zbiornika? Wybierz odpowiedź spośród podanych.
A) 8 m B) 18 m C) 2 m D) 6 m
Pan Henryk ma do wyboru dwa warianty abonamentu telefonicznego, których szczegóły przedstawiono w poniższej tabeli.
| Wariant I | Wariant II | |
| Miesięczny koszt abonamentu | 30 zł | 24 zł |
| Liczba darmowych minut w abonamencie | 30 | 20 |
| Koszt 1 minuty połączenia | 15 groszy | 20 groszy |
Pan Henryk średnio rozmawia przez telefon przez 90 minut w miesiącu. Który z wariantów abonamentu telefonicznego jest dla niego bardziej korzystny? Zapisz obliczenia.
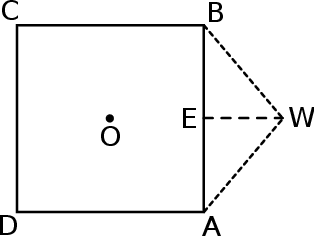
Na rysunku przedstawiono kwadrat 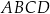 . Punkty
. Punkty 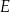 i
i 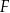 są środkami boków
są środkami boków 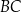 i
i 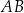 . Uzasadnij, że odcinki
. Uzasadnij, że odcinki 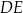 i
i 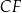 są prostopadłe.
są prostopadłe.

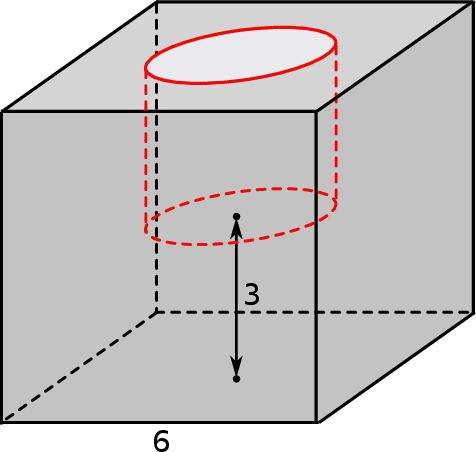
W sześcianie o krawędzi podstawy 6 wydrążono pionowy walec, którego wysokość i średnica są równe połowie długości krawędzi sześcianu. Oblicz pole powierzchni całkowitej tej bryły.