/Szkoła średnia/Zadania maturalne/Matura 2015/Matura próbna/Zadania.info
Próbny Egzamin Maturalny
z Matematyki Zestaw przygotowany przez serwis www.zadania.info poziom podstawowy
(technikum) 28 marca 2015 Czas pracy: 170 minut
Zadania zamknięte
Liczba 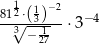 jest równa
jest równa
A) 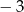 B)
B) 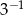 C)
C) 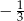 D) 3
D) 3
Pierwiastek równania 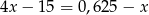 zaokrąglono do wartości 3,2. Błąd względny tego przybliżenia to
zaokrąglono do wartości 3,2. Błąd względny tego przybliżenia to
A) 2,4% B) 2,5% C) 7,5% D) 5%
Kąt  jest kątem ostrym i
jest kątem ostrym i 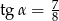 . Jaki warunek spełnia kąt
. Jaki warunek spełnia kąt  ?
?
A) 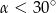 B)
B) 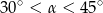 C)
C) 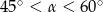 D)
D) 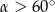
Wskaż nierówność, która opisuje przedział zaznaczony na osi liczbowej.
![]()
A) 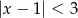 B)
B) 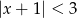 C)
C) 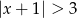 D)
D) 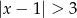
Para liczb 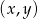 , która spełnia równanie
, która spełnia równanie 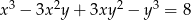 to
to
A) 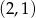 B)
B) 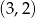 C)
C) 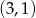 D)
D) 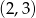
Liczba 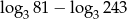 jest równa
jest równa
A) -2 B) -1 C) 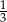 D) 3
D) 3
Suma kwadratów trzech początkowych wyrazów ciągu arytmetycznego o pierwszym wyrazie 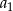 i różnicy
i różnicy  wyraża się wzorem
wyraża się wzorem
A) 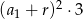 B)
B) 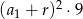 C)
C) 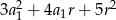 D)
D) 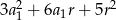
Do zbioru rozwiązań nierówności 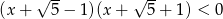 należy liczba
należy liczba
A) 0 B) 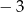 C)
C) 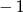 D) 3
D) 3
Zbiorem wartości funkcji, której wykres przedstawiono na rysunku jest przedział:
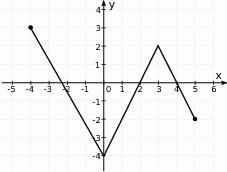
A) 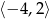 B)
B) 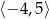 C)
C) 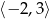 D)
D) 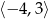
Jeżeli 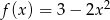 to funkcja
to funkcja 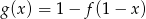 ma wzór
ma wzór
A) 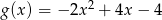
B) 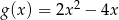
C) 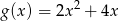
D) 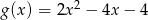
Na rysunku 1 jest przedstawiony wykres funkcji 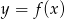 .
.
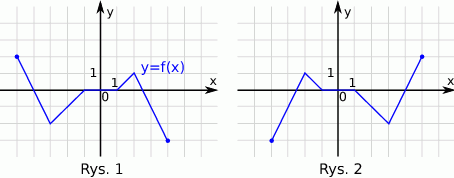
Funkcja przedstawiona na rysunku 2 jest określona wzorem
A) 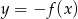 B)
B) 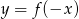 C)
C) 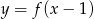 D)
D) 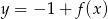
Dla 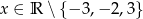 wyrażenie
wyrażenie 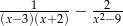 jest równe
jest równe
A) 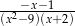 B)
B) 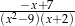 C)
C) 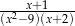 D)
D) 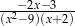
Liczba przekątnych sześciokąta foremnego jest równa
A) 9 B) 14 C) 18 D) 6
Miara kąta  jest równa:
jest równa:
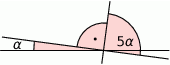
A) 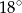 B)
B) 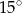 C)
C) 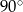 D)
D) 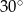
Ciąg 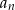 dany jest wzorem
dany jest wzorem 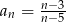 , gdzie
, gdzie 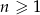 oraz
oraz 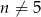 . Liczba wyrazów całkowitych tego ciągu to
. Liczba wyrazów całkowitych tego ciągu to
A) 1 B) 2 C) 3 D) 4
Punkt 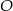 jest środkiem okręgu. Kąt środkowy
jest środkiem okręgu. Kąt środkowy 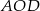 ma miarę
ma miarę
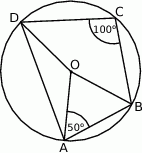
A) 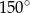 B)
B) 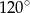 C)
C) 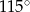 D)
D) 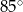
Dany jest romb o boku długości 4 i kącie ostrym 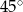 . Pole tego rombu jest równe
. Pole tego rombu jest równe
A) 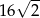 B)
B) 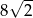 C) 16 D) 8
C) 16 D) 8
Wskaż równanie prostej, której fragment przedstawiony jest na poniższym wykresie
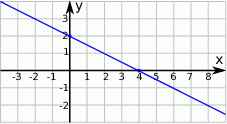
A) 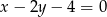 B)
B) 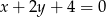 C)
C) 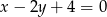 D)
D) 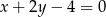
Długość odcinka  jest równa
jest równa
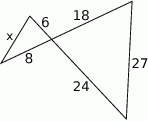
A) 9 B) 8 C) 12 D) 7,5
Równanie 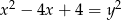 opisuje na płaszczyźnie
opisuje na płaszczyźnie
A) parabolę B) okrąg C) punkt D) dwie proste
Na loterii jest 20 losów, z których 8 jest wygrywających. Kupujemy jeden los. Prawdopodobieństwo zdarzenia, że nie wygramy nagrody jest równe
A)  B)
B)  C)
C)  D)
D) 
Suma miar kątów wewnętrznych wielokąta wypukłego jest równa 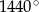 . Wynika stąd, że liczba boków tego wielokąta jest równa
. Wynika stąd, że liczba boków tego wielokąta jest równa
A) 5 B) 7 C) 10 D) 8
Odchylenie standardowe zestawu danych: 1, 2, 3, 4, 5 jest równe
A) 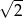 B) 2 C)
B) 2 C) 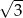 D) 3
D) 3
Każdą z sześciu krawędzi sześciokątnej ramki postanowiono pomalować na jeden z 10 kolorów, przy czym przeciwległe krawędzie mają mieć ten sam kolor, a żadne dwie sąsiednie krawędzie nie mogą mieć tego samego koloru. Liczba różnych możliwości pokolorowania ramki jest równa

A) 720 B) 1000 C) 30 D) 27
W graniastosłupie prawidłowym trójkątnym wszystkie krawędzie są tej samej długości. Suma długości wszystkich krawędzi jest równa 90. Wtedy pole powierzchni całkowitej tego graniastosłupa jest równe
A) 300 B) 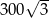 C)
C) 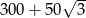 D)
D) 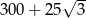
Zadania otwarte
Rozwiąż nierówność 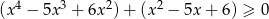 .
.
Na prostej 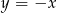 wyznacz punkt, który jest równo odległy od początku układu współrzędnych oraz od punktu
wyznacz punkt, który jest równo odległy od początku układu współrzędnych oraz od punktu 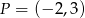 .
.
Na przyprostokątnych 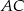 i
i 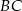 trójkąta prostokątnego
trójkąta prostokątnego 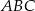 zbudowano trójkąty równoramienne
zbudowano trójkąty równoramienne 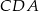 i
i 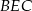 w ten sposób, że
w ten sposób, że 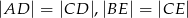 oraz punkty
oraz punkty 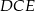 leżą na jednej prostej. Wykaż, że proste
leżą na jednej prostej. Wykaż, że proste 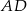 i
i 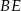 są równoległe.
są równoległe.
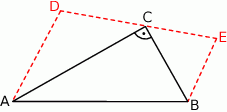
Wykaż, że jeżeli 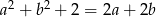 , to
, to 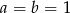 .
.
Czwarty wyraz ciągu arytmetycznego jest równy 8. Suma pięciu pierwszych wyrazów tego ciągu jest równa 15. Oblicz siódmy wyraz tego ciągu.
Spośród wierzchołków graniastosłupa sześciokątnego prostego losujemy jeden wierzchołek z dolnej podstawy i jeden wierzchołek z górnej podstawy. Oblicz prawdopodobieństwo tego, że wylosowane wierzchołki są końcami krawędzi bocznej graniastosłupa.
Pole podstawy ostrosłupa prawidłowego trójkątnego jest równe 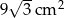 , a jego pole powierzchni bocznej jest równe
, a jego pole powierzchni bocznej jest równe 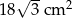 . Oblicz objętość tego ostrosłupa.
. Oblicz objętość tego ostrosłupa.
Dany jest trójkąt równoramienny 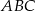 , w którym
, w którym 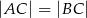 oraz
oraz 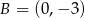 i
i 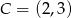 . Oś symetrii tego trójkąta ma równanie
. Oś symetrii tego trójkąta ma równanie 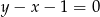 . Oblicz współrzędne wierzchołka
. Oblicz współrzędne wierzchołka 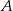 .
.
Dwie szkoły mają prostokątne boiska. Przekątna każdego boiska jest równa 65 m. Boisko w drugiej szkole ma długość o 4 m większą niż boisko w pierwszej szkole, ale szerokość o 8 m mniejszą. Oblicz długość i szerokość każdego z tych boisk.

