Zadanie nr 3925838
Uzasadnij, że liczba 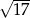 spełnia nierówność
spełnia nierówność 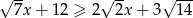 .
.
Rozwiązanie
Sposób I
Rozwiązujemy podaną nierówność. Ponieważ 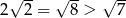 , wyrażenia z
, wyrażenia z  -em przenosimy na prawą stronę nierówności, a resztę liczb na lewą.
-em przenosimy na prawą stronę nierówności, a resztę liczb na lewą.
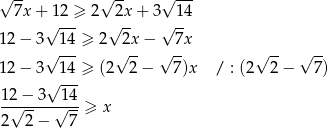
Usuwamy teraz niewymierność z mianownika.
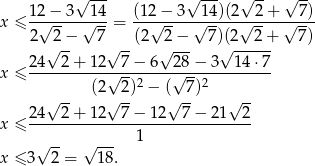
Oczywiście liczba 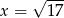 spełnia tę nierówność.
spełnia tę nierówność.
Sposób II
Podstawiamy w danej nierówności 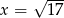 i przekształcamy tę nierówność w sposób równoważny.
i przekształcamy tę nierówność w sposób równoważny.
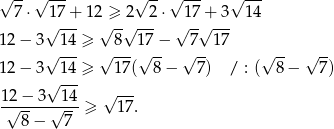
Usuwamy teraz niewymierność z mianownika.
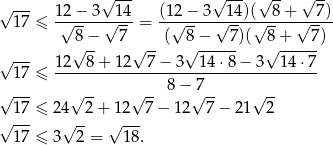
Otrzymana nierówność jest oczywiście spełniona, więc wyjściowa nierówność też musiała być prawdziwa.

