Zadanie nr 7019154
Wykaż, że dla dowolnych dodatnich liczb rzeczywistych  i
i 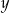 takich, że
takich, że 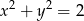 , prawdziwa jest nierówność
, prawdziwa jest nierówność 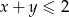 .
.
Rozwiązanie
Sposób I
Korzystamy z nierówności
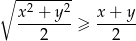
między średnimi: kwadratową i arytmetyczną. Mamy więc
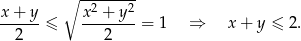
Sposób II
Przekształcamy daną nierówność w sposób równoważny.
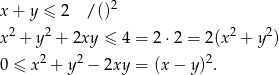
Otrzymana nierówność jest oczywiście prawdziwa, więc wyjściowa nierówność też musiała być prawdziwa.
Sposób III
Przekształcamy daną nierówność w sposób równoważny.
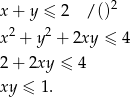
Liczby  i
i 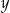 są dodatnie, więc możemy tę nierówność podnieść stronami do kwadratu.
są dodatnie, więc możemy tę nierówność podnieść stronami do kwadratu.
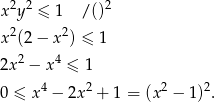
Otrzymana nierówność jest oczywiście prawdziwa, więc wyjściowa nierówność też musiała być prawdziwa.
Sposób IV
Tym razem zauważmy, że równanie 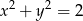 opisuje na płaszczyźnie okrąg o środku
opisuje na płaszczyźnie okrąg o środku 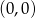 i promieniu
i promieniu 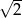 . Nierówność
. Nierówność 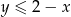 opisuje natomiast półpłaszczyznę znajdującą się pod prostą
opisuje natomiast półpłaszczyznę znajdującą się pod prostą 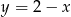 . Sprawdźmy, ile punktów wspólnych ma ta prosta z danym okręgiem.
. Sprawdźmy, ile punktów wspólnych ma ta prosta z danym okręgiem.
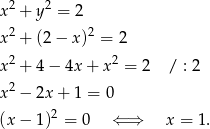
To oznacza, że prosta 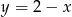 jest styczna do okręgu
jest styczna do okręgu 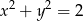 .
.
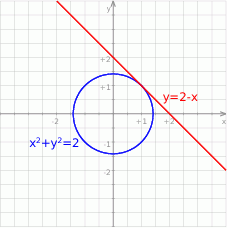
Gdy naszkicujemy tę sytuację, to widać, że wszystkie punkty tego okręgu rzeczywiście znajdują się poniżej prostej 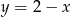 .
.

