Zadanie nr 3048784
Wykaż, że jeżeli 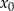 jest rozwiązaniem równania
jest rozwiązaniem równania 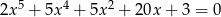 , to
, to 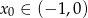 .
.
Rozwiązanie
Zagadnienie rozwiązania danego równania wygląda na dość beznadziejne, więc zamiast tego obliczmy pochodną wielomianu z lewej strony tak, aby zobaczyć jak zachowuje się ta funkcja.
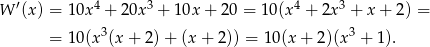
Widać teraz, że pochodna ma dwa miejsca zerowe 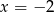 i
i 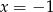 . Ponadto przy przejściu przez pierwsze z nich zmienia znak z dodatniego na ujemny, a przy przejściu przez drugie zmienia znak z ujemnego na dodatni. To oznacza, że funkcja
. Ponadto przy przejściu przez pierwsze z nich zmienia znak z dodatniego na ujemny, a przy przejściu przez drugie zmienia znak z ujemnego na dodatni. To oznacza, że funkcja 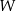 rośnie w przedziale
rośnie w przedziale 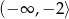 , potem maleje w przedziale
, potem maleje w przedziale 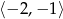 , a następnie ponownie rośnie w przedziale
, a następnie ponownie rośnie w przedziale 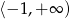 . Zauważmy jeszcze, że
. Zauważmy jeszcze, że
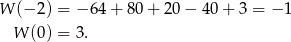
Z powyższej analizy wynika zatem, że funkcja 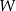 rośnie w przedziale
rośnie w przedziale 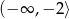 do wartości
do wartości 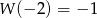 , następnie maleje w przedziale
, następnie maleje w przedziale 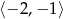 i potem cały czas rośnie. To oznacza, że na lewo od
i potem cały czas rośnie. To oznacza, że na lewo od 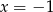 funkcja w całości znajduje się poniżej osi
funkcja w całości znajduje się poniżej osi 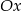 , a na prawo od
, a na prawo od 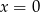 znajduje się w całości powyżej
znajduje się w całości powyżej 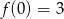 . To oznacza, że pierwiastek danego równania musi znajdować się w przedziale
. To oznacza, że pierwiastek danego równania musi znajdować się w przedziale 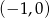 .
.
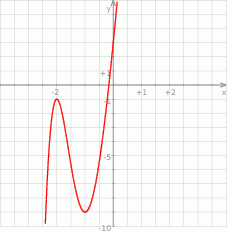
Na koniec, dla ciekawskich, wykres funkcji 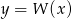 .
.